7 Die Evolution des Convolutional Neural Networks (CNN)

“Manchmal bringt die einfachste Idee die größte Innovation.” - William of Ockham, Philosoph

Das Convolutional Neural Network (CNN) zeigte bereits in den 1980er Jahren seine Möglichkeiten durch Yann LeCuns Forschung zu lernfähigen Faltungsfiltern mithilfe des Backpropagation-Algorithmus und der erfolgreichen Handschriftziffernerkennung durch LeNet-5 im Jahr 1998. Im Jahr 2012 gewann AlexNet den ImageNet Large Scale Visual Recognition Challenge (ILSVRC) mit überlegener Leistung und markierte damit das Beginnen des Deep-Learning-Zeitalters, insbesondere für CNNs. Nach AlexNet stießen jedoch Versuche, die Netzwerktiefe zu erhöhen, auf Schwierigkeiten aufgrund von Gradientenverschwindungs-/Explosion (vanishing/exploding gradients) Problemen.

2015 löste ResNet (Residual Network), das von Kaiming He und Kollegen aus dem Microsoft Research vorgeschlagen wurde, diese Herausforderung durch die revolutionäre Idee des “Restlernens (residual learning)”. ResNet trainierte erfolgreich ein 152-schichtiges Netzwerk, was zuvor unmöglich schien, und setzte damit neue Standards in der Bilderkennung. Die Residuerverbindung (residual connection), die Kernkomponente von ResNet, ist heute in den meisten Deep-Learning-Architekturen ein wesentlicher Bestandteil.

In diesem Kapitel untersuchen wir die Entstehungsgründe und die Entwicklung des CNNs und analysieren detailliert die Kernideen, Struktur und Implementierungsmethoden von ResNet. Darüber hinaus behandeln wir auch wichtige Meilensteine in der Entwicklung des CNNs wie das Inception-Modul und die Kernkonzepte von EfficientNet, um ein breites Verständnis für die Evolution moderner CNN-Architekturen zu vermitteln.

7.1 Die Entstehung des Convolutional Neural Networks

Herausforderung: Wie kann man einen Computer dazu bringen, Objekte in einem Bild so zu erkennen wie ein Mensch?

Forscherfrust: Frühe Forscher der Computervisualisierung suchten nach Methoden, um Merkmale (features) aus Bildern zu extrahieren und diese als Grundlage für die Objekerkenntnis zu nutzen, anstatt einfach nur auf Pixelwerte zu verweisen. Es war jedoch nicht klar, welche Merkmale wichtig sind und wie man sie effizient extrahieren kann.

Anfang der 1960er Jahre entdeckten David Hubel und Torsten Wiesel durch Experimente mit der visuellen Rinde von Katzen, dass bestimmte Neuronen nur auf spezifische visuelle Muster (wie vertikale Linien, horizontale Linien oder Kanten in bestimmter Richtung) selektiv reagieren. Obwohl Hubel und Wiesel für diese Forschung den Nobelpreis für Physiologie oder Medizin im Jahr 1981 erhielten, konnte damals niemand voraussehen, dass ihre Entdeckung zu revolutionären Fortschritten im Bereich der künstlichen Intelligenz führen würde. Die Arbeiten von Hubel und Wiesel bildeten die biologische Grundlage für zwei zentrale Konzepte des modernen CNNs: die Faltungsschicht (convolutional layer) und die Poolungsschicht (pooling layer).

• Einfache Zellen (Simple cells): Reagieren auf lokale Merkmale wie Kanten oder Linien in bestimmter Richtung. Dies ist vergleichbar mit der Art, wie die Faltungsschicht eines CNNs durch Filter (Kerne) lokale Merkmale aus einem Bild extrahiert.
• Komplexe Zellen (Complex cells): Haben eine Positionsinvarianz (translation invariance) gegenüber den Ausgaben einfacher Zellen. Das bedeutet, sie reagieren, egal an welcher Stelle des Bildes ein bestimmtes Muster auftritt. Dies ähnelt der Art und Weise, wie die Poolungsschicht eines CNNs die Größe von Merkmalskarten reduziert, während es gleichzeitig die Positionsinformation zu einem gewissen Grad beibehält. 1980, schlug Kunihiko Fukushima auf der Grundlage dieser Konzepte den Neocognitron vor, der als Vorläufer des CNN angesehen werden kann. Der Neocognitron besteht aus mehreren Schichten von S-Zellen (Simple Zelle) und C-Zellen (Complex Zelle), die hierarchische Merkmale von Bildern extrahieren und robuste Mustererkennung bei Positionsversionen durchführen können.

Allerdings musste der damalige Neocognitron, da kein Lernalgorithmus etabliert war, die Filter (Gewichte) manuell eingestellt werden. 1989 führte Yann LeCun den Backpropagation-Algorithmus in Convolutional Neural Networks ein und ermöglichte es, die Filter automatisch aus Daten zu lernen. Dadurch entstand das moderne CNN, und LeNet-5 zeigte herausragende Leistungen bei der Erkennung von Handschriftzahlen.

2012 gewann AlexNet den ImageNet Challenge durch seine überlegene Leistung und eröffnete die Ära des Deep Learnings, insbesondere der CNNs. AlexNet verfügte über eine viel tiefergehende und komplexere Struktur als LeNet-5 und konnte durch die Nutzung von GPU paralleler Berechnungen effizient auf großen Datensätzen (ImageNet) trainiert werden.

7.1.1 Die Entwicklung der digitalen Signalverarbeitung und die Hintergründe von CNN

Um Computer Vision und CNNs tiefer zu verstehen, ist es notwendig, den Entwicklungsprozess des Bereichs Digital Signal Processing (DSP) zu betrachten. 1807 schlug Joseph Fourier vor, dass jede periodische Funktion in eine Summe aus Sinus- und Cosinusfunktionen zerlegt werden kann – die Fourierreihe. Dies bildete den Grundstein für das Gebiet der Signalverarbeitung und ermöglichte es, Signale im Zeitbereich (time domain) in den Frequenzbereich (frequency domain) zu transformieren und sie zu analysieren.

Insbesondere ermöglichten die Fortschritte in der Entwicklung digitaler Computer in den 1960er Jahren die Erfindung des schnellen Fourierransforms (Fast Fourier Transform, FFT), was eine neue Ära für die digitale Signalverarbeitung einleitete. Die FFT ermöglichte es, die Fourier-Transformation viel schneller zu berechnen und führte dazu, dass Signalverarbeitungstechniken in verschiedenen Bereichen wie Bildverarbeitung, Sprachverarbeitung und Kommunikation weit verbreitet wurden.

In der Bildverarbeitung spielt die Faltung eine zentrale Rolle. Die Faltung ist ein grundlegender Vorgang, bei dem ein Filter (Kernel) auf das Eingangssignal (Bild) angewendet wird, um gewünschte Merkmale zu extrahieren oder Rauschen zu reduzieren. Seit den 1960er Jahren haben sich digitale Filtertheorien entwickelt und es ermöglichten Prozesse wie Kantenentdeckung (edge detection), Verschärfung (sharpening) und Verweichlichung (blurring). In der späten 1960er Jahre wurde der Kalman-Filter eingeführt, der ein leistungsfähiges Werkzeug zur Schätzung des Zustands eines Systems auf Grundlage verrauschter Messwerte bereitstellte. Der Kalman-Filter verwendet einen rekursiven Algorithmus basierend auf dem Bayes-Theorem und wird heute im Computer Vision-Bereich für Objekterkennung (object tracking) und Robotersehen unerlässlich eingesetzt.

Diese traditionellen digitalen Signalverarbeitungstechniken bildeten die theoretische Grundlage von CNNs. Allerdings mussten die vorhandenen Filter manuell entwickelt werden und hatten eine feste Form, wodurch ihre Fähigkeit, verschiedene Muster zu erkennen, begrenzt war. CNNs überwanden diese Einschränkungen, indem sie es ermöglichten, die optimalen Filter automatisch aus Daten zu lernen, was eine Revolution im Bereich der Bilderkennung brachte.

7.1.2 Digitale Filter und Faltung

Um CNNs zu verstehen, muss man zunächst das Konzept digitaler Filter begreifen. Digitale Filter werden in der Signalverarbeitung zu zwei Hauptzwecken verwendet. 1. Signalseparation: Aus einem gemischten Signal nur die gewünschten Signalanteile trennen (z. B. wenn der Herzschlag eines Fetus und der Herzschlag der Mutter vermischt sind, nur den Herzschlag des Fetus trennen). 2. Signalrestauration: Verformte oder beschädigte Signale so weit wie möglich wiederherstellen (z. B. Rauschreduktion in Bildern, Schärfung von unscharfen Bildern).

Einer der grundlegendsten digitalen Filter ist der Sobel-Filter. Der Sobel-Filter ist eine 3x3-Matrix und wird verwendet, um Kanten (edges) in Bildern zu erkennen.

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

import numpy as np
# Sobel filter for vertical edge detection
sobel_vertical = np.array([
    [-1, 0, 1],
    [-2, 0, 2],
    [-1, 0, 1]
])

# Sobel filter for horizontal edge detection
sobel_horizontal = np.array([
    [-1, -2, -1],
    [ 0,  0,  0],
    [ 1,  2,  1]
])

Zuerst betrachten wir, wie ein klassischer digitaler Filter funktioniert. Der gesamte Code befindet sich in chapter_06/filter_utils.py.

import matplotlib.pyplot as plt
from dldna.chapter_07.filter_utils import show_filter_effects, create_convolution_animation
%matplotlib inline

# 테스트용 이미지 URL
IMAGE_URL = "https://raw.githubusercontent.com/opencv/opencv/master/samples/data/building.jpg"

# 필터 효과 시각화
show_filter_effects(IMAGE_URL)

Der obige Beispiel verwendet die folgenden Filter.

filters = {
    'Gaussian Blur': cv2.getGaussianKernel(3, 1) @ cv2.getGaussianKernel(3, 1).T,
    'Sharpen': np.array([
        [0, -1, 0],
        [-1, 5, -1],
        [0, -1, 0]
    ]),
    'Edge Detection': np.array([
        [-1, -1, -1],
        [-1, 8, -1],
        [-1, -1, -1]
    ]),
    'Emboss': np.array([
        [-2, -1, 0],
        [-1, 1, 1],
        [0, 1, 2]
    ]),
    'Sobel X': np.array([
        [-1, 0, 1],
        [-2, 0, 2],
        [-1, 0, 1]
    ])
}

Diese Filter arbeiten auf die Weise, die als Faltung (Convolution) bekannt ist. Die Filter werden über das Bild geschoben (sliding), und an jeder Position wird die Summe der elementweisen Multiplikationen (element-wise multiplication) zwischen Filter und Bildausschnitt berechnet. Dies kann durch folgende Gleichung dargestellt werden:

\((I * K)(x, y) = \sum_{i=-a}^{a}\sum_{j=-b}^{b} I(x+i, y+j)K(i, j)\)

Dabei ist \(I\) das Eingangsbild, \(K\) der Kern (Filter). \((x,y)\) sind die Koordinaten des Ausgabepixels, \((i,j)\) sind die Koordinaten innerhalb des Kernels, und \(a\) und \(b\) sind jeweils halbe Breite/Höhe des Kernels.

Die Faltungsoperation ist visuell leichter zu verstehen. Die folgende Animation zeigt den Prozess der Faltung:

from dldna.chapter_07.conv_visual import create_conv_animation
from IPython.display import HTML
%matplotlib inline

# 애니메이션 생성 및 표시
animation = create_conv_animation()

# js_html = animation.to_jshtml()
# display(HTML(f'<div style="width:700px">{js_html}</div>'))

# html_video = animation.to_html5_video()
# display(HTML(f'<div style="width:700px">{html_video}</div>'))

display(animation)

Once Loop Reflect

Die größten Grenzen eines digitalen Filters liegen in seinen festgelegten Eigenschaften. Traditionelle Filter wie Sobel und Gaussian sind manuell so entworfen, dass sie nur bestimmte Muster erkennen können, was ihre Fähigkeit einschränkt, komplexe und vielfältige Muster zu erkennen. Sie sind außerdem anfällig für Veränderungen in der Größe oder Rotation von Bildern und können keine Merkmale aus mehreren Ebenen automatisch lernen. Diese Einschränkungen führten zur Entwicklung von CNNs, die lernfähige Filter auf Datenbasis sind.

7.1.2 Eigenschaften und Struktur von CNNs

CNNs imitieren das biologische Sehverarbeitungsmechanismus, um die räumliche Hierarchie (spatial hierarchy) in Bildern effizient zu lernen.

Lernfähige Filter (Learnable Filters)

Die wichtigste Eigenschaft von CNNs ist die Verwendung von automatisch aus Daten gelernten Filtern, anstelle traditionell manuell entworfener Filter (z. B. Sobel, Gabor-Filter). Dies ermöglicht es CNNs, spezielle Aufgaben (wie Bildklassifizierung, Objekt-Erkennung) optimal angepasste Merkmalsextraktoren selbst zu lernen.

import torch
import torch.nn as nn
import torch.nn.functional as F

class SimpleCNN(nn.Module):
    def __init__(self):
        super().__init__()
        # Multiple learnable filters: 32 (channels) of 3x3 filter weight matrices + 32 biases
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
        # Multiple learnable filters: For 32 input channels, 64 output channels of 3x3 filter weight matrices + 64 biases
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        return x

In der SimpleCNN-Beispiel sind conv1 und conv2 jeweils Faltungs-Layer mit lernfähigen Filtern. Das erste Argument von nn.Conv2d ist die Anzahl der Eingangskanäle, das zweite Argument ist die Anzahl der Ausgabekanäle (Anzahl der Filter), kernel_size ist die Größe des Filters und padding füllt den Rand des Eingangsbildes mit Nullen, um die Größe des Ausgabe-Feature-Maps zu regulieren.

Hierarchische Merkmalsextraktion (Hierarchical Feature Extraction)

CNNs extrahieren durch mehrere Schichten von Faltungs- und Pooling-Operationen hierarchische Merkmale aus Bildern.

• Anfangsschicht (Low-level features): Grundlegende visuelle Merkmale wie Kanten, Linien und Farbänderungen werden erkannt.
• Mittlere Schicht (Mid-level features): Mittelstufige Merkmale wie Textur, Muster und einfache Formen werden gelernt.
• Letzte Schicht (High-level features): Abstrakte und hochstufige Merkmale wie Teile von Objekten oder die allgemeine Struktur von Objekten werden erkannt.

Diese hierarchische Merkmalsextraktion ähnelt der Art, wie das menschliche visuelle System visuelle Informationen schrittweise verarbeitet.

import torch
import torch.nn as nn
import torch.nn.functional as F

class HierarchicalCNN(nn.Module):
    def __init__(self):
        super().__init__()
        # Low-level feature extraction
        self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
        self.bn1 = nn.BatchNorm2d(64)

        # Mid-level feature extraction
        self.conv2 = nn.Conv2d(64, 128, 3, padding=1)
        self.bn2 = nn.BatchNorm2d(128)

        # High-level feature extraction
        self.conv3 = nn.Conv2d(128, 256, 3, padding=1)
        self.bn3 = nn.BatchNorm2d(256)

    def forward(self, x):
        # Low-level features (edges, textures)
        x = F.relu(self.bn1(self.conv1(x)))

        # Mid-level features (patterns, partial shapes)
        x = F.relu(self.bn2(self.conv2(x)))

        # High-level features (object parts, overall structure)
        x = F.relu(self.bn3(self.conv3(x)))
        return x

Dieses HierarchicalCNN-Beispiel zeigt ein CNN, das drei Faltungs-Layer verwendet, um niedrigstufige, mittelstufige und hochstufige Merkmale zu extrahieren. In der Praxis werden oft viel mehr Layer gestapelt, um komplexere Merkmale zu lernen.

Räumliche Hierarchie (Spatial Hierarchy) und Pooling

Jede Schicht eines CNNs besteht in der Regel aus einer Faltung, einer Aktivierungsfunktion (z.B. ReLU) und einem Pooling-Vorgang.

• Faltungs-Layer: Extrahieren von Merkmalen aus den Eingabe-Merkmalskarten mit Hilfe von Filtern.
• Aktivierungsfunktion: Fügt der Netzstruktur Nichtlinearität hinzu, indem sie eine nichtlineare Funktion wie ReLU anwendet.
• Pooling-Layer: Reduziert die Größe der Merkmalskarte (Downsampling), um die Berechnungsmenge zu verringern und Translation Invariance zu verstärken. Das bedeutet, dass ein Objekt auch dann erkannt werden kann, wenn es sich innerhalb eines Bildes leicht verschiebt. Oft wird Max-Pooling verwendet.

Dank dieser strukturellen Eigenschaften können CNNs die räumlichen Informationen in Bildern effektiv lernen und robuste Merkmale extrahieren, die unabhängig von der Position des Objekts im Bild sind.

Parameter-Sharing (Parameter-Teilen)

Parameter-Sharing ist ein wesentlicher Effizienzmechanismus in CNNs. Der gleiche Filter wird an allen Positionen des Eingangsbildes (oder der Merkmalskarte) angewendet. Dies basiert auf der Annahme, dass die gleichen Merkmale an jeder Position erkannt werden sollen. (z.B. ein Senkrechter-Linien-Filter erkennt vertikale Linien sowohl in der oberen linken als auch in der unteren rechten Ecke des Bildes)

1. Speicher-Effizienz: Da die Parameter eines Filters an allen Positionen geteilt werden, verringert sich die Anzahl der Modellparameter drastisch. Zum Beispiel hat ein Faltungs-Layer mit 64 Filtern von 3x3 Größe auf einem 32x32 Farbbild (3 Kanäle) jeweils 3x3x3 = 27 Parameter. Ohne Parameter-Sharing müssten an jeder der 32x32 Positionen unterschiedliche Filter verwendet werden, was insgesamt (32x32) x (3x3x3) x 64 Parameter erfordern würde. Mit Parameter-Sharing sind jedoch nur 27 x 64 + 64 (Bias) = 1792 Parameter erforderlich.

2. Statistische Effizienz: Da der gleiche Filter Merkmale an verschiedenen Positionen des Bildes lernt, können wirkungsvolle Merkmalsextraktoren mit weniger Parametern gelernt werden. Dies verbessert die Generalisierungsleistung des Modells.

3. Paralleler Prozess: Da der Faltungsvorgang für jeden Filter unabhängig durchgeführt wird und die Ergebnisse dann zusammengefasst werden, ist er sehr geeignet für parallele Verarbeitung.

from dldna.chapter_07.param_share import compare_parameter_counts, show_example

# 다양한 입력 크기에 따른 비교. CNN 입출력 채널을 1로 고정.
input_sizes = [8, 16, 32, 64, 128]
comparison = compare_parameter_counts(input_sizes)
print("\nParameter Count Comparison:")
print(comparison)

# 32x32 입력에 대한 상세 예시
show_example(32)

Parameter Count Comparison:
  Input Size  Conv Params  FC Params  Ratio (FC/Conv)
0        8x8           10       4160            416.0
1      16x16           10      65792           6579.2
2      32x32           10    1049600         104960.0
3      64x64           10   16781312        1678131.2
4    128x128           10  268451840       26845184.0

Example with 32x32 input:
CNN parameters: 10 (fixed)
FC parameters: 1,049,600
Parameter reduction: 99.9990%

Akzeptanzbereich (Receptive Field)

Der Akzeptanzbereich (receptive field) bezieht sich auf die Größe des Eingabebildbereichs, der die Ausgabe eines bestimmten Neurons beeinflusst. In CNNs wächst der Akzeptanzbereich schrittweise, während die Eingabe durch die Faltungsschichten und Pooling-Schichten verarbeitet wird.

• Anfangsschichten: Da sie einen kleinen Akzeptanzbereich haben, erkennen sie lokale Merkmale (z. B. Kanten, Punkte).
• Tiefe Schichten: Da sie einen breiten Akzeptanzbereich haben, berücksichtigen sie ein größeres Kontextumfeld und lernen abstrakte Merkmale (z. B. Teile von Objekten, gesamte Objekte).

Dank dieser hierarchischen Merkmalsextraktion und des wachsenden Akzeptanzbereichs können CNNs in der Bilderkennung hervorragende Leistungen erzielen.

Zusammenfassend lässt sich sagen, dass CNNs durch Kernmerkmale wie Faltungsberechnungen, Pooling-Operationen, lernfähige Filter, Parameterfreigabe und hierarchische Merkmalsextraktion, inspiriert von biologischen Sehverarbeitungssystemen, in den Bereichen Bilderkennung und Computer Vision innovative Fortschritte bewirkt haben.

7.1.3 Mathematische Darstellung und Implementierung von CNNs

Die mathematische Darstellung eines CNN lautet wie folgt:

\((F * K)(p) = \sum_{s+t=p} F(s)K(t) = \sum_{i}\sum_{j} F(i,j)K(p_x-i, p_y-j)\)

Hierbei steht \(F\) für die Eingabe-Feature-Map und \(K\) für den Kernel. In der praktischen Implementierung müssen mehrere Kanäle und Batch-Bearbeitung berücksichtigt werden, weshalb es wie folgt erweitert wird:

\(Y_{n,c_{out},h,w} = \sum_{c_{in}}\sum_{i=0}^{k_h-1}\sum_{j=0}^{k_w-1} X_{n,c_{in},h+i,w+j} \cdot W_{c_{out},c_{in},i,j} + b_{c_{out}}\)

Hierbei: - \(n\) ist der Batch-Index - \(c_{in}\), \(c_{out}\) sind die Eingangs-/Ausgangskanäle - \(h\), \(w\) sind Höhe und Breite - \(k_h\), \(k_w\) sind die Kernelgrößen - \(W\) sind die Gewichte, \(b\) ist der Bias

Die Klasse chapter_06/simple_conv.py implementiert 2D-Konvolution und Max-Pooling basierend auf dem PyTorch-Quellcode für Lernzwecke. Sie verwendet ausbildungsbezogene Zwecke und verzichtet auf CUDA-Optimierung sowie auf Exception-Handling und ähnliches. Da der Quellcode detaillierte Kommentare enthält, werde ich die Erklärung der Klasse hier weglassen.

import torch
import matplotlib.pyplot as plt
from dldna.chapter_07.simple_conv import SimpleConv2d, SimpleMaxPool2d
# %matplotlib inline  # This line is only needed in Jupyter/IPython environments

# Input data creation (e.g., 1 image, 1 channel, 6x6 size)
x = torch.tensor([
    [1, 2, 3, 4, 5, 6],
    [7, 8, 9, 10, 11, 12],
    [13, 14, 15, 16, 17, 18],
    [19, 20, 21, 22, 23, 24],
    [25, 26, 27, 28, 29, 30],
    [31, 32, 33, 34, 35, 36]
], dtype=torch.float32).reshape(1, 1, 6, 6)

# SimpleConv2d test
conv = SimpleConv2d(in_channels=1, out_channels=2, kernel_size=3, padding=1)
conv_output = conv(x)

# SimpleMaxPool2d test
pool = SimpleMaxPool2d(kernel_size=2)
pool_output = pool(x)

# Visualize results
fig, axes = plt.subplots(1, 3, figsize=(15, 5))

# Original image
axes[0].imshow(x[0, 0].detach().numpy(), cmap='viridis')
axes[0].set_title('Original Image')

# Convolution result (first channel)
axes[1].imshow(conv_output[0, 0].detach().numpy(), cmap='viridis')
axes[1].set_title('Conv2d Output (Channel 0)')

# Pooling result
axes[2].imshow(pool_output[0, 0].detach().numpy(), cmap='viridis')
axes[2].set_title('MaxPool2d Output')

for ax in axes:
    ax.axis('off')
plt.tight_layout()
plt.show()

# Print output sizes
print("Input size:", x.shape)
print("Convolution output size:", conv_output.shape)
print("Pooling output size:", pool_output.shape)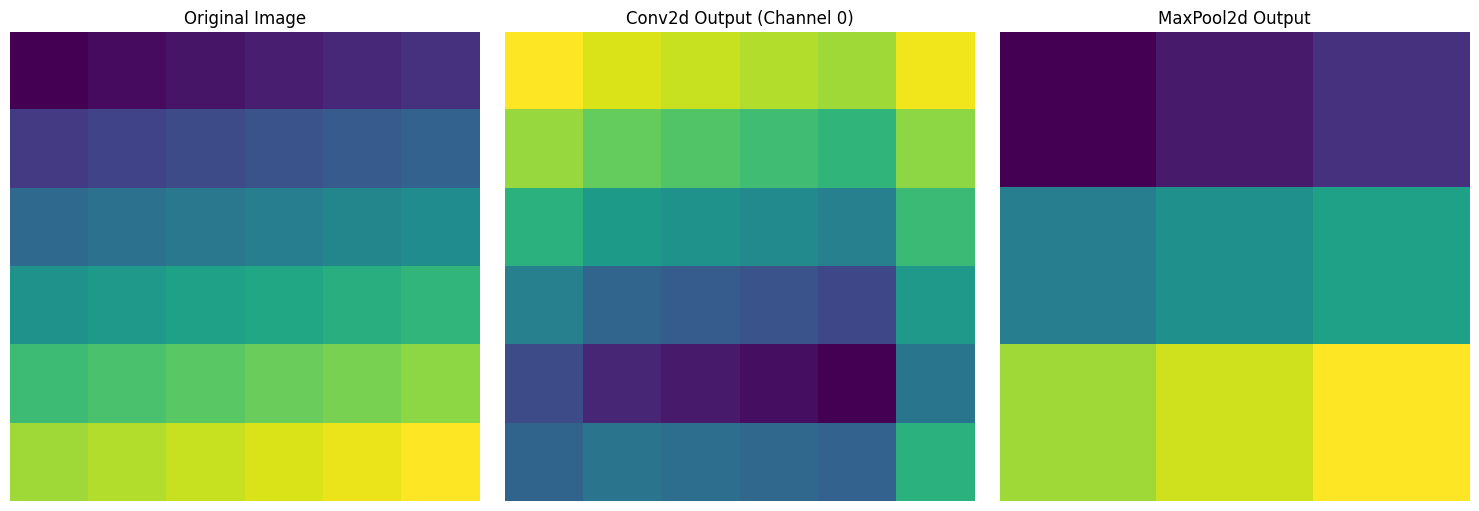

Input size: torch.Size([1, 1, 6, 6])
Convolution output size: torch.Size([1, 2, 6, 6])
Pooling output size: torch.Size([1, 1, 3, 3])

Für ein Eingabebild der Größe 6x6 wurden drei Ergebnisse visualisiert. Links ist das originale Bild, in dem die Werte von 1 bis 36 sequenziell zunehmen, in der Mitte das Resultat nach Anwendung eines 3x3-Faltungsfilters und rechts das Resultat nach Anwendung des Max-Poolings mit einer Größe von 2x2, bei dem sich die Größe halbiert hat.

Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Frequenzbereichsinterpretation der Faltung und Bedeutung von 1x1-Faltungen)

Interpretation des Faltungsvorgangs im Frequenzbereich und Bedeutung der 1x1-Faltung

Wir interpretieren den Faltungsvorgang, eine Kernoperation in CNNs, im Frequenzbereich und untersuchen insbesondere die tiefer gehende Bedeutung der 1x1-Faltung. Durch Fourier-Transformation und das Faltungstheorem erforschen wir die verborgenen Aspekte des Faltungsvorgangs.

1. Wiederholung des Faltungsvorgangs

Wir wiederholen kurz den Faltungsvorgang, wie in Abschnitt 7.1.2 und 7.1.3 besprochen. Die Faltung von einem zweidimensionalen Bild \(I\) mit einem Kern (Filter) \(K\), \(I * K\), ist wie folgt definiert:

\((I * K)[i, j] = \sum_{m} \sum_{n} I[i-m, j-n] K[m, n]\)

Hierbei sind \(i\), \(j\) die Positionen der Pixel im Ausgabebild, und \(m\), \(n\) sind die Positionen der Pixel im Kern. Die diskrete Faltung (discrete convolution) besteht darin, den Kern über das Bild zu verschieben, die Elemente der überschneidenden Bereiche zu multiplizieren und die Summe dieser Produkte zu berechnen.

2. Einführung in die Fourier-Transformation

Die Fourier-Transformation ist ein mächtiges Werkzeug, um Signale aus dem Zeitbereich (raumlichen Bereich) in den Frequenzbereich zu transformieren.

• Zeitbereich vs. Frequenzbereich: Der Zeitbereich repräsentiert die Form von Signalen, wie wir sie normalerweise wahrnehmen (z.B. Änderungen der Pixelwerte eines Bildes über die Zeit). Der Frequenzbereich zeigt an, aus welchen Frequenzkomponenten das Signal besteht (z.B. verschiedene räumliche Frequenzkomponenten in einem Bild).

• Definition der Fourier-Transformation: Die Fourier-Transformation zerlegt ein Signal in eine Summe von Sinus- und Kosinusfunktionen mit verschiedenen Frequenzen und Amplituden. Für eine kontinuierliche Funktion \(f(t)\) ist die Fourier-Transformation \(\mathcal{F}\{f(t)\} = F(\omega)\) wie folgt definiert.

  \(F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt\)

  Hierbei ist \(j\) die imaginäre Einheit und \(\omega\) die Winkelgeschwindigkeit. Die inverse Fourier-Transformation (Inverse Fourier Transform) transformiert ein Signal aus dem Frequenzbereich zurück in den Zeitbereich.

  \(f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{j\omega t} d\omega\)

• Diskrete Fourier-Transformation (DFT) & Schnelle Fourier-Transformation (FFT): Da Computer keine kontinuierlichen Signale verarbeiten können, wird die diskrete Fourier-Transformation (Discrete Fourier Transform, DFT) verwendet. Die schnelle Fourier-Transformation (Fast Fourier Transform, FFT) ist ein effizienter Algorithmus zur Berechnung der DFT. Die Formel für die DFT lautet wie folgt:

\(X[k] = \sum_{n=0}^{N-1} x[n] e^{-j(2\pi/N)kn}\), \(k = 0, 1, ..., N-1\)

Hierbei ist \(x[n]\) das diskrete Signal, \(X[k]\) das Ergebnis der DFT und \(N\) die Länge des Signals.

3. Faltungstheorem (Convolution Theorem)

Das Faltungstheorem beschreibt eine wichtige Beziehung zwischen dem Faltungsvorgang und der Fourier-Transformation. Der Kernaspekt ist, dass die Faltung im Zeitbereich im Frequenzbereich zu einer einfachen Multiplikation wird.

• Faltungstheorem: Die Fourier-Transformation der Faltung zweier Funktionen \(f(t)\) und \(g(t)\) entspricht dem Produkt ihrer Fourier-Transformierten.

  \(\mathcal{F}\{f * g\} = \mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\)

  Das bedeutet, wenn \(F(\omega)\) und \(G(\omega)\) die Fourier-Transformierten von \(f(t)\) und \(g(t)\) sind, dann ist die Fourier-Transformation von \(f(t) * g(t)\) gleich \(F(\omega)G(\omega)\).

• Interpretation in the frequency domain: The convolution theorem allows us to interpret convolution operations in the frequency domain. Convolution filters play a role in emphasizing or suppressing specific frequency components of the input signal. Multiplication in the frequency domain is equivalent to adjusting the amplitude of the corresponding frequency component.

4. Frequency Response of Convolution Filters

By analyzing the frequency response of various convolution filters, we can determine which frequency components are passed and which are blocked by the filter.

• Visualization of the frequency response: The Fourier transform of the filter can be calculated to obtain the frequency response. The frequency response is typically represented by magnitude and phase. Magnitude indicates the amplitude change of each frequency component, while phase represents the phase change.

• Filter types:

  • Low-pass filter (low-frequency pass filter): Passes low-frequency components and blocks high-frequency components. It has a blurring effect on images (e.g., Gaussian filter).
  • High-pass filter (high-frequency pass filter): Passes high-frequency components and blocks low-frequency components. It has an edge-enhancing effect on images (e.g., Sobel filter).
  • Band-pass filter (band-pass filter): Passes only a specific frequency band and blocks the rest.

The following is an example of visualizing the frequency response of the Sobel filter and Gaussian filter. (Running the code will generate images.)

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve2d

def plot_frequency_response(kernel, title):
    # Calculate the 2D FFT of the kernel
    kernel_fft = np.fft.fft2(kernel, s=(256, 256)) # Zero-padding for better visualization
    kernel_fft_shifted = np.fft.fftshift(kernel_fft) # Shift zero frequency to center

    # Calculate the magnitude and phase
    magnitude = np.abs(kernel_fft_shifted)
    phase = np.angle(kernel_fft_shifted)

    # Plot the magnitude response
    plt.figure(figsize=(12, 6))
    plt.subplot(1, 2, 1)
    plt.imshow(np.log(1 + magnitude), cmap='gray') # Log scale for better visualization
    plt.title(f'{title} - Magnitude Response')
    plt.colorbar()
    plt.axis('off')


    #Plot the phase response
    plt.subplot(1, 2, 2)
    plt.imshow(phase, cmap='hsv')
    plt.title(f'{title} - Phase Response')
    plt.colorbar()
    plt.axis('off')
    plt.show()

5.1x1 Faltung im Frequenzbereich interpretieren

1x1 Faltung behält räumliche Informationen bei und führt Berechnungen zwischen Kanälen durch.

• Linearkombination von Kanälen: 1x1 Faltung bildet lineare Kombinationen der Kanäle an jeder Pixelposition. Dies kann im Frequenzbereich als gewichtete Summe der Frequenzkomponenten jedes Kanals interpretiert werden. Das heißt, die Gewichte des 1x1 Faltungsfilters repräsentieren die Bedeutung der Frequenzkomponenten jedes Kanals.

• Anpassung von Korrelationen und Neuaufbau von Merkmalen: 1x1 Faltung passt die Korrelation (Korrelation) zwischen den Kanälen an. Sie kombiniert Kanäle mit starken Korrelationen oder entfernt unnötige Kanäle, um die Merkmalsdarstellung neu aufzubauen.

• Rolle in Inception-Modulen: 1x1 Faltung spielt in Inception-Modulen zwei wichtige Rollen.

  • Dimensionsreduktion: Die Anzahl der Kanäle wird reduziert, um die Berechnungsmenge zu verringern.
  • Hinzufügen von Nichtlinearität: Nach 1x1 Faltung werden nichtlineare Aktivierungsfunktionen wie ReLU angewendet, um die Ausdruckskraft des Modells zu steigern. Aus der Perspektive der Frequenzantwort kann dies dazu führen, dass Kanäle mit unterschiedlichen Frequenzantworten gemischt und eine komplexere Frequenzantwort erzeugt wird.

7.1.4 Berechnung der lernbaren Parameter von CNNs

Die Berechnung der Anzahl der lernbaren Parameter eines CNNs ist für die Netzwerkdesign- und Optimierung sehr wichtig. Wir betrachten dies Schritt für Schritt.

1. Basis-Konvolutionsschicht

conv = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3)

Die Parameterberechnung ist wie folgt: - Größe jedes Filters: 3 × 3 × 1 (Kerngröße² × Eingangskanäle) - Anzahl der Filter: 32 (Ausgangskanäle) - Bias: 32 (gleich der Anzahl der Ausgangskanäle) - Gesamtanzahl der Parameter = (3 × 3 × 1) × 32 + 32 = 320

2. Max-Pooling-Schicht

maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

• Keine lernbaren Parameter
• Führt nur die Operation durch, das Maximum in einem 2×2-Bereich zu wählen
• Die Größe der Feature Maps wird nur reduziert (Höhe und Breite jeweils um den Faktor 1/2)

3. Konvolution mit Padding

conv = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, padding=1)

Padding beeinflusst nur die Ausgabegröße und ändert die Anzahl der Parameter nicht. - Größe jedes Filters: 3 × 3 × 3 - Anzahl der Filter: 64 - Gesamtanzahl der Parameter = (3 × 3 × 3) × 64 + 64 = 1,792

4. Kombination von Konvolution mit Stride und Pooling

conv = nn.Conv2d(in_channels=64, out_channels=128, kernel_size=3, stride=2)
maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

• Konvolutionsparameter = (3 × 3 × 64) × 128 + 128 = 73,856
• Pooling-Parameter = 0
• Gesamtanzahl der Parameter = 73,856

Berechnung der Ausgabegröße.

Konvolution-Ausgabegröße = ((Einganggröße + 2×Padding - Kerngröße) / Stride) + 1
Pooling-Ausgabegröße = ((Einganggröße - Poolinggröße) / Pooling-Stride) + 1

5. Beispiel für eine komplexe Struktur (Grundblock von ResNet)

class BasicBlock(nn.Module):
    def __init__(self, in_channels=64, out_channels=64):
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.maxpool = nn.MaxPool2d(kernel_size=2, stride=2)

Parameterberechnung. 1. Erste Faltung: (3 × 3 × 64) × 64 + 64 = 36.928 2. Erste Batch-Normalisierung: 64 × 2 = 128 (Gamma und Beta) 3. Zweite Faltung: (3 × 3 × 64) × 64 + 64 = 36.928 4. Zweite Batch-Normalisierung: 64 × 2 = 128 5. Max-Pooling: 0

Gesamtanzahl der Parameter = 74.112

Diese Berechnung der Anzahl der Parameter ist sehr wichtig, um die Komplexität des Modells zu verstehen, die Speicheranforderungen vorherzusagen und das Risiko von Überanpassung (Overfitting) zu bewerten. Insbesondere helfen Pooling-Schichten, indem sie ohne zusätzliche Parameter die Größe der Feature-Maps effektiv reduzieren und so die Berechnungs-effizienz erhöhen.

7.1.5 CNN: Lernen von Merkmalsextraktion und Abstraktion

Der Kern der CNNs liegt darin, durch “lernfähige Filter” Merkmale aus Bildern zu extrahieren und diese hierarchisch zu kombinieren, um abstraktere Darstellungen zu lernen. Dieser Prozess beginnt mit den spezifischen Details eines Bildes und führt zu einem Schritt, bei dem abstrakte Bedeutungen (z.B. Art der Objekte) erfasst werden, und kann in zwei wesentliche Aspekte unterteilt werden.

1. Extraktion und Transformation von Bildmerkmalen (Feature Extraction and Transformation): Merkmale aus lokalen Bereichen eines Bildes werden extrahiert und durch nichtlineare Aktivierungsfunktionen nur relevante Merkmale beibehalten.
2. Zunahme der Filter (Kanäle) und Erweiterung des abstrakten Raums (Increasing Filters and Expanding Abstract Space): Je tiefer die Schichten werden, desto mehr Filter (Kanäle) werden hinzugefügt, um vielfältigere und abstraktere Merkmale zu lernen.

1. Extraktion und Transformation von Bildmerkmalen

Die Faltungs-Ebenen der CNNs wenden lernfähige Filter auf die Eingangsbilder (oder die Merkmalskarten aus vorherigen Schichten) an, um Merkmale zu extrahieren. Jeder Filter wird so trainiert, dass er bestimmte Muster in einem Bild (z.B. Kanten, Texturen, Formen) erkennt. Dieser Prozess besteht aus den folgenden Schritten.

• Faltungsberechnung: Die Filter interagieren mit lokalen Bereichen des Bildes (Rezeptionsfeldern), um Werte zu generieren, die angaben, ob bestimmte Muster in diesen Bereichen vorhanden sind. Durch diesen Prozess werden Merkmalskarten (feature maps) erstellt, die die Stärke der von den Filtern erkannten Muster an jeder Position im Bild darstellen.
• Aktivierungsfunktion: Die Ergebnisse der Faltungsberechnung (die Merkmalskarten) passieren eine nichtlineare Aktivierungsfunktion wie ReLU. Die Aktivierungsfunktion überträgt nur Merkmale, die einen bestimmten Schwellenwert überschreiten, an die nächste Schicht und ignoriert alle anderen Merkmale. Dies ermöglicht es dem Netzwerk, sich auf wichtige Merkmale zu konzentrieren und unnötige Informationen zu entfernen (Sparsamkeit).
• Erweiterung des abstrakten Raums: Die Anzahl der Filter (Kanäle) wird erhöht, um die Vielfalt der Merkmale zu erhöhen.

2. Zunahme der Filter (Kanäle) und Erweiterung des abstrakten Raums

Mit jedem Durchgang durch eine Schicht verringert sich die räumliche Größe der Merkmalskarten (rasterartige Dimension: Breite, Höhe) in der Regel, während die Anzahl der Filter (Kanäle) zunimmt. Dies ist ein zentrales Mechanismus für das Lernen von Abstraktion durch CNNs.

• Verringerte räumliche Größe: Faltungsberechnungen (Stride > 1) oder Pooling-Vorgänge verringern die räumliche Größe der Merkmalskarten. Dies reduziert den Rechenaufwand und verstärkt die Positionsinvarianz, d.h., Objekte werden auch dann erkannt, wenn sie in einem Bild leicht verschoben sind.
• Erhöhte Anzahl von Kanälen: Jede Faltungsschicht verwendet mehrere Filter, um verschiedene Aspekte der Eingangsmerkmalskarten zu erfassen.
  • Frühe Schichten: Erkennen von niedrigstufigen Merkmalen wie Kanten und Farbveränderungen. Diese niedrigstufigen Merkmale repräsentieren die grundlegenden Bestandteile eines Bildes.
  • Mittlere Schichten: Kombination der niedrigstufigen Merkmale aus frühen Schichten, um mittlerniveau Merkmale wie Texturen, Muster und einfache Formen zu erkennen.
  • Tiefe Schichten: Kombination der Merkmale aus vorherigen Schichten, um Teile von Objekten (Augen, Nase, Mund usw.), oder sogar die Objekte selbst (Personen, Autos, Tiere usw.) und hochstufige, abstrakte Merkmale zu erkennen. Die Erhöhung der Anzahl von Filtern (Kanälen) bedeutet, dass die Dimension der Merkmale, die CNNs zur Darstellung von Bildern verwenden, zunimmt. Während frühe Schichten sich auf konkrete Details des Bildes konzentrieren, lernen tiefere Schichten Informationen, die für das Verstehen abstrakter Bedeutungen im Bild notwendig sind. Dies ähnelt dem Prozess, bei dem Menschen Objekte betrachten: Zu Beginn fokussieren sie sich auf detaillierte Teile und erfassen allmählich die gesamte Form und Bedeutung.

Beispiel für CNN-Schichtstruktur (VGGNet):

Das folgende Diagramm zeigt die Architektur von VGGNet. VGGNet ist ein repräsentatives Modell, das systematisch den Einfluss der Tiefe von CNNs auf die Leistung untersucht hat.

• Architektur von VGGNet:

VGG16-Architektur.
Quelle: K. Simonyan, A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv:1409.1556, 2014.

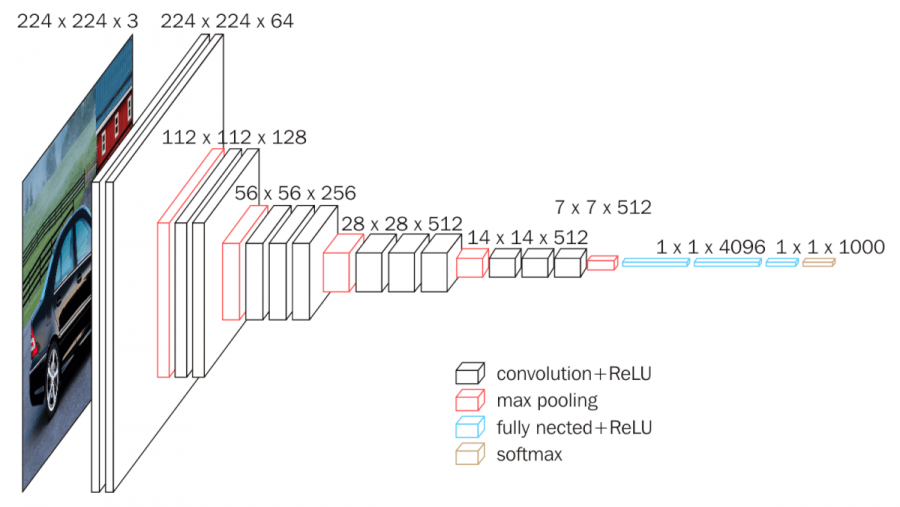
Wie im Diagramm zu sehen ist, besteht VGGNet aus mehreren Convolutional Layers und Pooling-Layers, die aufeinander gestapelt sind. Bei jedem Durchgang durch eine Schicht verringert sich die räumliche Größe der Feature Maps und die Anzahl der Kanäle nimmt zu. Dies veranschaulicht visuell den Prozess, bei dem CNNs Bilder von niedrigdimensionalen konkreten Darstellungen (Pixelwerte) zu hochdimensionalen abstrakten Darstellungen (Art des Objekts) umwandeln.

Zusammenfassend kann man sagen, dass die “lernfähigen Filter” der CNNs mächtige Werkzeuge sind, um Merkmale von Bildern zu extrahieren und diese hierarchisch zu kombinieren, um abstraktere Darstellungen zu lernen. Durch mehrere Schichten von Convolutional- und Pooling-Operationen transformiert ein CNN Bilder in kleinere, tiefere und abstraktere Darstellungen, wobei es während dieses Prozesses die für das Verstehen der Bedeutung von Bildern aus den Daten entscheidenden Informationen lernt. Diese Fähigkeit zur Merkmalsextraktion und Abstraktion ist der zentrale Grund dafür, dass CNNs in verschiedenen Computer-Vision-Aufgaben wie Bilderkennung, Objekterkennung und Bildsegmentierung ausgezeichnete Leistungen erzielen.

::: {.callout-note collapse=“true” title=“Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Die verschiedenen Bedeutungen des Begriffs”Kernel” im Deep Learning und Maschinelles Lernen)“} ## Deep Learning und Maschinelles Lernen: Verschiedene Bedeutungen des Terms”Kernel”

“Wörter haben an sich selbst keine Bedeutung, sondern nur im Kontext.” - (Grundprinzip der Semantik/Pragmatik)

Beim Studium von Deep Learning, maschinellem Lernen und Signalverarbeitung stößt man häufig auf den Begriff “Kernel” (Kern). Der Begriff “Kernel” kann je nach Kontext völlig unterschiedliche Bedeutungen haben, was für Anfänger verwirrend sein kann. In diesem Deep Dive werden wir die verschiedenen Kontexte und Bedeutungen von “Kernel” klar definieren und die Beziehungen zwischen den einzelnen Verwendungen untersuchen.

1. Kernel in Convoluational Neural Networks (CNNs) (Faltungskern)

In CNNs wird der Begriff Filter synonym mit Kernel verwendet. Ein Faltungsschicht (convolutional layer) führt eine Faltungsoperation auf Eingabedaten (Bild oder Merkmalskarte) durch, indem sie einen kleinen Matrix über die Daten bewegt.

• Funktion: Es extrahiert Merkmale aus lokalen Bereichen des Bildes (receptive field).

• Arbeitsweise: Der Kernel bewegt sich über die Eingabedaten (Stride), multipliziert die Pixelwerte der überlappenden Region mit den Gewichten des Kernels und addiert alle Werte (Faltung). Dieser Prozess erzeugt einen Wert, der anzeigt, wie stark das von dem Kernel zu erkennende Muster (z. B. Kanten, Texturen) an dieser Position ausgeprägt ist.

• Lernbar: In CNNs werden die Gewichte des Kernels durch den Rückwärtspropagation Algorithmus aus den Daten gelernt. Das bedeutet, dass ein CNN den Kernel so anpasst, um die für das gegebene Problem (z. B. Bildklassifizierung) nützlichsten Merkmale zu extrahieren.

• Beispiel: Sobel-Kernel

  $

  \[\begin{bmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{bmatrix}\]

  $ Dieser 3x3-Sobel-Kernel wird verwendet, um vertikale Kanten in Bildern zu erkennen.

• Kernaspekt: Der Kernel in CNNs ist ein lernfähiger Parameter, der die Funktion hat, lokal begrenzte Merkmale aus Bildern zu extrahieren.

2. Kernel in Support Vector Machines (SVM) (Kernel-Funktion, Kernel-Trick)

In SVMs (Support Vector Machine) ist der Begriff “Kernel” eine Funktion, die die Ähnlichkeit zwischen zwei Datenpunkten berechnet. Ein SVM kartiert Daten auf einen hochdimensionalen Merkmalsraum (feature space), um nichtlineare Klassifikationsprobleme zu lösen. Der Kernel-Trick ist eine Technik, bei der diese hochdimensionale Kartierung nicht explizit berechnet wird, sondern durch die Verwendung einer Kernel-Funktion das Skalarprodukt im hochdimensionalen Raum implizit berechnet wird.

• Funktion: Daten werden in einen hochdimensionalen Merkmalsraum kartiert, um nichtlineare Klassifikationsprobleme in lineare Klassifikationsprobleme zu transformieren.
• Kernaspekt: Es ermöglicht die effiziente Berechnung des Skalarprodukts im hochdimensionalen Merkmalsraum (ohne explizite Kartierung).
• Mathematische Darstellung: \(K(\mathbf{x}, \mathbf{y}) = \phi(\mathbf{x}) \cdot \phi(\mathbf{y})\)
  • \(K(\mathbf{x}, \mathbf{y})\): Kernel-Funktion (Ähnlichkeit zwischen den beiden Eingangsvektoren \(\mathbf{x}\), \(\mathbf{y}\))
  • \(\phi(\mathbf{x})\): Funktion, die den Eingangsvektor \(\mathbf{x}\) in den hochdimensionalen Merkmalsraum kartiert
  • \(\cdot\): Skalarprodukt
• Typische Kernelfunktionen:
  • Linearkernel (Linear Kernel): \(K(\mathbf{x}, \mathbf{y}) = \mathbf{x}^T \mathbf{y}\) (einfaches Skalarprodukt)
  • Polynomieller Kernel (Polynomial Kernel): \(K(\mathbf{x}, \mathbf{y}) = (\gamma \mathbf{x}^T \mathbf{y} + r)^d\)
  • RBF-Kernel (Radial Basis Function Kernel, Gaußscher Kernel): \(K(\mathbf{x}, \mathbf{y}) = \exp(-\gamma \|\mathbf{x} - \mathbf{y}\|^2)\) (am weitesten verbreitet)
  • Sigmoid-Kernel: \(K(\mathbf{x}, \mathbf{y}) = \tanh(\gamma \mathbf{x}^T \mathbf{y} + r)\)
• Kern: Der Kernel im SVM misst die Ähnlichkeit zwischen Datenpunkten und löst nichtlineare Probleme durch eine implizite Abbildung in einen hochdimensionalen Merkmerraum.

3. Kerne in der Wahrscheinlichkeitsrechnung und Statistik (Kernel Density Estimation)

In der Wahrscheinlichkeitsrechnung und Statistik ist ein Kernel eine nichtnegative Funktion, die symmetrisch um den Ursprung ist und einen Funktionswert von 1 hat. KDE (Kernel Density Estimation) ist eine parameterfreie Methode, die auf gegebenen Daten (Stichproben) basiert, um eine Wahrscheinlichkeitsdichtefunktion zu schätzen.

• Rolle: Es wird als “Gewichtsfunktion” verwendet, um die Dichte in der Umgebung von Datenpunkten zu schätzen.
• Kern: Kernel-Funktionen werden überlagert, um eine glatte (smooth) Darstellung der gesamten Datendistribution zu erzeugen.
• Mathematische Darstellung: \(\hat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right)\)
  • \(\hat{f}(x)\): geschätzte Wahrscheinlichkeitsdichte an der Stelle \(x\)
  • \(n\): Anzahl der Datenpunkte
  • \(h\): Bandbreite (bandwidth) - Parameter, um die “Breite” des Kernels zu steuern (Glättungsparameter)
  • \(K(\cdot)\): Kernel-Funktion
  • \(x_i\): \(i\)-ter Datenpunkt
• Typische Kernelfunktionen:
  • Gaußscher Kernel (Gaussian Kernel): \(K(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2}\) (am weitesten verbreitet)
  • Epanechnikov-Kernel: \(K(x) = \frac{3}{4}(1 - x^2) \text{ if } |x| \le 1\)
  • Uniformer Kernel (Box Kernel): \(K(x) = \frac{1}{2} \text{ if } |x| \le 1\)
• Kern: In KDE dient der Kernel als Gewichtsfunktion, um eine Wahrscheinlichkeitsdichtefunktion zu schätzen.

4. Betriebssystemkernels (Operating System Kernels)

In der Informatik, insbesondere im Bereich Betriebssysteme, ist ein Kernel ein zentrales Bestandteil des Betriebssystems. Er dient als Schnittstelle zwischen Hardware und Anwendungen und arbeitet auf der tiefsten Ebene des Systems.

• Rolle:
  • Prozessverwaltung
  • Speicherverwaltung
  • Dateisystemverwaltung
  • Eingabe-/Ausgabeverwaltung (I/O)
  • Verwaltung von Hardware-Ressourcen
• Beispiele: Linux-Kernel, Windows NT-Kernel, XNU-Kernel von macOS

Zusammenfassung und Vergleich

Bereich	Bedeutung des Kernels	Kernrolle
CNN	Filter, der Faltungsoperationen ausführt (lernbare Gewichtsmatrix)	Extraktion lokaler Merkmale in Bildern
SVM	Funktion, die die Ähnlichkeit zwischen zwei Datenpunkten berechnet (implizite Abbildung in einen hochdimensionalen Merkmaraum)	Nichtlineare Daten werden in einem hochdimensionalen Raum abgebildet, um linear trennbar zu sein
Wahrscheinlichkeit/Statistik (KDE)	Gewichtsfunktion zur Schätzung der Wahrscheinlichkeitsdichte	Glatte Schätzung der Datenverteilung
Betriebssystem	Kernkomponente des Betriebssystems (Schnittstelle zwischen Hardware und Anwendungen)	Systemressourcen-Management, Hardwareabstraktion
Lineare Algebra	Nullraum einer linearen Abbildung (oder Matrix), d. h. die Menge der Vektoren \(\mathbf{x}\), die \(A\mathbf{x}=\mathbf{0}\) erfüllen (für eine lineare Abbildung \(T:V→W\) ist \(\text{Ker}(T)=\{\mathbf{v}∈V∣T(\mathbf{v})=\mathbf{0}\}\))	Charakterisierung der Eigenschaften einer linearen Abbildung

In Deep Learning, insbesondere bei CNNs, bezieht sich “Kern” in den meisten Fällen auf einen FaltungsfILTER. Allerdings sollte man sich daran erinnern, dass der Begriff im Kontext anderer Maschinenlernverfahren wie SVMs oder Gaußsche Prozesse auch für Kernfunktionen verwendet werden kann. Es ist wichtig, den genauen Sinn von “Kern” je nach Kontext zu verstehen. :::

7.2 Erscheinen von ResNet

Herausforderung: Wie kann die Tiefe eines neuronalen Netzwerks effektiv erhöht werden, ohne dabei Probleme mit verschwindenden oder explodierenden Gradienten zu haben und das Lernen stabil zu gestalten?

Kopfschmerzen der Forscher: Da CNNs in der Bilderkennung ausgezeichnete Leistungen zeigten, versuchten die Forscher, tiefere Netze zu bauen. Allerdings führte eine zunehmende Tiefe des Netzwerks während des Backpropagation-Prozesses zu Problemen mit verschwindenden (vanishing gradients) oder explodierenden Gradienten (exploding gradients), wodurch das Lernen nicht ordnungsgemäß erfolgte. Einfache lineare Transformationen begrenzten die Ausdrucksfähigkeit tiefer Netze. Wie kann man diese grundlegenden Grenzen überwinden und die Tiefe von neuronalen Netzwerken optimal nutzen?

Als CNNs im Bereich der Bilderkennung überraschenderweise erfolgreich waren, fragten sich die Forscher natürlich, ob “tiefere Netzwerke nicht bessere Leistungen erzielen könnten”. Theoretisch sollten tiefere Netze in der Lage sein, komplexere und abstraktere Merkmale zu lernen. In der Praxis stellte sich jedoch heraus, dass das Training-Fehler (training error) mit zunehmender Tiefe des Netzwerks tatsächlich zunahm.

7.2.1 Probleme tiefer Neuronaler Netze und die Entstehung von ResNet

Im Jahr 2015 veröffentlichte ein Microsoft-Team (Kaiming He et al.) einen bahnbrechenden Lösungsansatz für dieses Problem in einem Paper. Sie zeigten experimentell, dass die Schwierigkeit des Trainings tiefer Neuronaler Netze nicht auf Overfitting, sondern auf Optimierungsprobleme zurückzuführen ist, bei denen die Fehler selbst bei den Trainingsdaten nicht ordnungsgemäß reduziert werden konnten.

Das Team beobachtete, dass ein 56-schichtiges Neuronales Netzwerk bei Trainingsdaten einen größeren Fehler zeigte als ein 20-schichtiges Netz. Dies war ein widersprüchliches Ergebnis im Vergleich zur Intuition, dass das 56-schichtige Netzwerk zumindest die Leistung des 20-schichtigen Netzes erreichen sollte (das 56-schichtige Netzwerk könnte die Funktion des 20-schichtigen Netzes erlernen, wenn die restlichen 36 Schichten eine Identitätsabbildung lernen). Somit stellte sich die grundlegende Frage: “Warum sind tiefere Neuronale Netze nicht in der Lage, selbst einfache Identitätsabbildungen zu erlernen?”

Um dieses Problem zu lösen, schlug das Team einen sehr einfachen aber mächtigen Ansatz vor: Residuenlern (Residual Learning). Der Kerngedanke ist, dass die Eingabe \(x\) direkt zum Output eines Layers hinzugefügt wird.

Residualverbindung (Residual Connection / Skip Connection):

Die Implementierung der Idee des Residuens Lernens ist die Residualverbindung oder Skip-Verbindung. Eine Residualverbindung schafft einen direkten Pfad, um die Eingabe \(x\) zum Output eines Layers hinzuzufügen.

Intuitives Verständnis von ResNet:

Die Residualverbindungen in ResNet ähneln den Rückkopplungsschaltungen (feedback circuits) der Elektrotechnik. Auch wenn das Eingangssignal beim Durchgang durch die Schichten verzerrt oder abgeschwächt wird, kann das ursprüngliche Signal unverändert weitergeleitet werden, sodass Informationen (und Gradienten) ohne Verlust durch das Netzwerk fließen können.

Erfolg von ResNet: ResNet hat durch residuelles Lernen und Skip-Verbindungen erfolgreich sehr tiefe Netze trainiert, die zuvor unmöglich waren, wie zum Beispiel ein 152-schichtiges Netz. Als Ergebnis gewann es den ILSVRC (ImageNet Large Scale Visual Recognition Challenge) Wettbewerb 2015 mit einem erstaunlichen Fehlerrate von 3,57%, die unterhalb der menschlichen Fehlerquote (ca. 5%) lag.

Die residuellen Verbindungen von ResNet sind eine einfache, aber sehr mächtige Idee, die den späteren Fortschritten in der Deep-Learning-Architektur stark zugeschrieben wird.

• Transformer (2017): Die Transformer-Architektur, die eine Revolution im Bereich des Natural Language Processing auslöste, hat Skip-Verbindungen von ResNet in Form von “Add & Norm” Layern übernommen.
• DenseNet (2017): DenseNet hat die Idee von ResNet erweitert und “dichte Verbindungen” verwendet, bei denen jede Schicht mit den Ausgaben aller vorherigen Schichten direkt verbunden ist.
• Inception-ResNet: Ein Modell, das die Inception-Module von GoogLeNet und die residuellen Verbindungen von ResNet kombiniert.
• EfficientNet, MobileNetV2: Leichtgewichtige Netze wie EfficientNet und MobileNetV2 haben ebenfalls das Konzept des residuellen Lernens von ResNet übernommen.

7.2.2 Struktur und Kernaspekte von ResNet

ResNet besteht hauptsächlich aus zwei Arten von Blöcken, nämlich dem Basisblock (Basic Block) und dem Flaschenhalsblock (Bottleneck Block).

• Basisblock (Basic Block): Wird in ResNet-18 und ResNet-34 verwendet. Er besteht aus zwei 3x3 Faltungsschichten, wobei nach jeder Faltungsschicht Batch-Normalisierung und die ReLU-Aktivierungsfunktion folgen. Und der wichtigste Aspekt ist die Residualverbindung, die den Input dieser beiden Schichten zum Output hinzufügt.

import torch
import torch.nn as nn
import torch.nn.functional as F

class BasicBlock(nn.Module):
    """Basic block for ResNet
    Consists of two 3x3 convolutional layers
    """
    expansion = 1  # Output channel expansion factor

    def __init__(self, in_channels, out_channels, stride=1):
        super().__init__()
        # First convolutional layer
        self.conv1 = nn.Conv2d(in_channels, out_channels,
                              kernel_size=3, stride=stride, padding=1)
        self.bn1 = nn.BatchNorm2d(out_channels)

        # Second convolutional layer
        self.conv2 = nn.Conv2d(out_channels, out_channels * self.expansion,
                              kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels * self.expansion)

        # Skip connection (adjust dimensions with 1x1 convolution if necessary)
        self.shortcut = nn.Sequential()
        if stride != 1 or in_channels != out_channels * self.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels * self.expansion,
                         kernel_size=1, stride=stride),
                nn.BatchNorm2d(out_channels * self.expansion)
            )

    def forward(self, x):
        # Main path
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))

        # Add skip connection
        out += self.shortcut(x)
        out = F.relu(out)
        return out

• Residualverbindung (Residual Connection): out += self.shortcut(x) ist der Kern. Das Eingangssignal wird direkt zur Ausgabe addiert.
• Dimensionsanpassung: Wenn die Anzahl der Eingangs- und Ausgangskanäle unterschiedlich ist oder der Stride nicht 1 ist, so dass sich die Größe der Featuremaps ändert, wird eine 1x1-Faltung über self.shortcut angewendet, um die Kanalanzahl und Größe anzupassen.

Flaschenhalsblock (Bottleneck Block)

Wird in ResNet-50 und höher verwendet. Dient der effizienten Erstellung tiefer Netzwerke. Es besteht aus einer Kombination von 1x1, 3x3 und 1x1 Faltungen, wobei die Anzahl der Kanäle zunächst reduziert und dann wieder erhöht wird, ähnlich wie ein Flaschenhals.

class Bottleneck(nn.Module):
    """병목(Bottleneck) 구조 구현"""
    
    expansion = 4  # 출력 채널을 4배로 확장하는 상수

    def __init__(self, in_channels, out_channels, stride=1):
        """
        Args:
            in_channels: 입력 채널 수
            out_channels: 중간 처리 채널 수 (최종 출력은 이것의 expansion배)
            stride: 스트라이드 크기 (기본값: 1)
        """
        super().__init__()

        # 1단계: 1x1 컨볼루션으로 채널 수를 줄임 (차원 감소)
        # 예: 256 -> 64 채널로 감소
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=1)
        self.bn1 = nn.BatchNorm2d(out_channels)
        
        # 2단계: 3x3 컨볼루션으로 특징 추출 (병목 구간)
        # 감소된 채널 수로 연산 수행 (예: 64채널에서 처리)
        self.conv2 = nn.Conv2d(out_channels, out_channels, 
                              kernel_size=3, stride=stride, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channels)
        
        # 3단계: 1x1 컨볼루션으로 채널 수를 다시 늘림 (차원 복원)
        # 예: 64 -> 256 채널로 확장 (expansion=4인 경우)
        self.conv3 = nn.Conv2d(out_channels, 
                              out_channels * self.expansion, kernel_size=1)
        self.bn3 = nn.BatchNorm2d(out_channels * self.expansion)

Die Bottleneck-Struktur hat, wie der Name schon sagt, eine Form, bei der die Dimension der Kanäle zunächst eingeschränkt und dann wieder erweitert wird. Angenommen, wir haben eine Feature Map mit 256 Eingangskanälen:

1. Die erste 1x1-Konvolution verringert die Dimension von 256→64.
2. Die 3x3-Konvolution wird auf den reduzierten 64 Kanälen durchgeführt.
3. Die letzte 1x1-Konvolution stellt die Dimension von 64→256 wieder her.

Diese Struktur hat folgende Vorteile: - Reduzierte Berechnungsmenge: Die kostspieligste 3x3-Konvolution wird auf wenigen Kanälen durchgeführt. - Reduzierte Anzahl der Parameter: Die Gesamtanzahl der Parameter ist im Vergleich zu einem Basismodul erheblich geringer. - Erhalt der Ausdrucksfähigkeit: Bei der Verringerung der Dimension werden die Fähigkeiten zur Lernung verschiedener Merkmale bewahrt.

Aufgrund dieser Effizienz wird in tiefen Modellen ab ResNet-50 die Bottleneck-Struktur anstelle des Basismoduls verwendet.

Es gibt zwei Formen von Skip-Verbindungen. Wenn die Anzahl der Eingangs- und Ausgangskanäle gleich ist, werden sie direkt verbunden. Bei unterschiedlichen Kanalzahlen wird eine 1x1-Konvolution verwendet, um die Kanalzahl anzupassen. Dies wurde von den Inception-Modulen des GoogLeNet (2014) inspiriert.

ResNet stapelt mehrere dieser grundlegenden Blöcke oder Bottleneck-Blöcke, um ein tiefes Netzwerk zu bilden.

ResNet gibt es in verschiedenen Versionen abhängig von der Tiefe des Netzwerks (ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152 usw.).

• ResNet-18, ResNet-34: Verwenden das grundlegende Blockschema (Basic Block).
• ResNet-50, ResNet-101, ResNet-152: Verwenden das Flaschenhalsblockschema (Bottleneck Block).

Die allgemeine Struktur von ResNet ist wie folgt:

1. Anfängliche Faltungsschicht: Eine 7x7-Faltung und Max-Pooling werden verwendet, um die Größe der Eingabebilder zu reduzieren.
2. Mehrere Stufen (Stage): Jede Stufe besteht aus mehreren Blöcken (entweder grundlegenden Blöcken oder Flaschenhalsblöcken). Bei dem ersten Block jeder Stufe wird der Stride auf 2 gesetzt, um die Größe der Merkmalskarten zu halbieren (Downsampling).
3. Durchschnittspooling (Average Pooling): Entfernt die räumlichen Dimensionen der Merkmalskarten. (Global Average Pooling)
4. Vollverbindungsschicht (Fully Connected Layer): Führt die Klassifikation durch.

Netzwerktiefe und Anzahl der Blöcke:

Die Tiefe von ResNet wird durch die Anzahl der Blöcke in jeder Stufe bestimmt. Zum Beispiel verwendet ResNet-18 2 grundlegende Blöcke pro Stufe ([2, 2, 2, 2]). ResNet-50 verwendet [3, 4, 6, 3] Flaschenhalsblöcke pro Stufe.

• ResNet-18:
  • Anfängliche 7x7-Faltung: 1 Schicht
  • Grundlegender Block (2 3x3-Faltungen): 2 Schichten x (2 + 2 + 2 + 2) = 16 Schichten
  • Endgültige vollverbindende Schicht: 1 Schicht
  • Insgesamt 1 + 16 + 1 = 18 Schichten

# 총 층수 = 1 + (2 × 2 + 2 × 2 + 2 × 2 + 2 × 2) + 1 = 18
def ResNet18(num_classes=10):
    return ResNet(BasicBlock, [2, 2, 2, 2], num_classes) # 기본 블록 사용

• ResNet-50:
  • Anfängliche 7x7-Faltung: 1 Schicht
  • Engflaschenblock (3 Faltungen): 3 Schichten x (3 + 4 + 6 + 3) = 48 Schichten
  • Endgültige voll verbundene Schicht: 1 Schicht
  • Gesamt 1 + 48 + 1 = 50 Schichten

# 병목 블록: 1x1 → 3x3 → 1x1 구조
# 총 층수 = 1 + (3 × 3 + 3 × 4 + 3 × 6 + 3 × 3) + 1 = 50
def ResNet50(num_classes=10):
    return ResNet(Bottleneck, [3, 4, 6, 3], num_classes) # 병목 블록 사용

ResNet-Designprinzipien:

• 4 Stufen: In jeder Stufe wird die Größe der Feature Maps halbiert und die Anzahl der Kanäle verdoppelt. Dies folgt dem Designkonzept von VGGNet.
• Mehr Blöcke in mittleren Stufen platzieren: Üblicherweise werden mehr Blöcke in der mittleren Stufe (Stufe 3) platziert. Dies basiert auf empirischen Beweisen, dass mittlere Ebene Features für die Objekterkennung wichtig sind.
• Bottleneck-Struktur (tiefe Netzwerke): Mit zunehmender Tiefe des Netzwerks wird die Bottleneck-Struktur zur Verbesserung der Rechen-effizienz verwendet.

Dank dieser strukturellen Innovationen konnte ResNet sehr tiefe Netzwerke effizient lernen, was den Standard für moderne Deep-Learning-Architekturen wurde. Die Ideen von ResNet beeinflussten verschiedene abgeleitete Modelle wie Wide ResNet, ResNeXt und DenseNet.

7.2.4 Trainieren und Visualisierung der Merkmalsextraktion von ResNet

Ein Beispiel für das Training des ResNet-18-Modells mit dem FashionMNIST-Datensatz befindet sich in chapter_07/train_resnet.py.

from dldna.chapter_07.train_resnet import train_resnet18, save_model

model = train_resnet18(epochs=10)
# Save the model
save_model(model)

Lassen Sie uns tatsächlich überprüfen, wie ResNet die Merkmale eines Bildes extrahiert. Wir werden ein trainiertes ResNet-18-Modell verwenden, um zu visualisieren, wie sich die Merkmalskarten bei jedem Schichtdurchgang verändern.

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from dldna.chapter_07.resnet import ResNet18
from dldna.chapter_07.train_resnet import get_trained_model_and_test_image
from torchvision import datasets, transforms

%matplotlib inline

def visualize_features(model, image):
    """각 층의 특징 맵을 시각화하는 함수"""
    features = {}
    
    # 특징 맵을 저장할 훅 등록
    def get_features(name):
        def hook(model, input, output):
            features[name] = output.detach()
        return hook

    # 각 주요 층에 훅 등록
    model.conv1.register_forward_hook(get_features('conv1'))
    for idx, layer in enumerate(model.layer1):
        layer.register_forward_hook(get_features(f'layer1_{idx}'))
    for idx, layer in enumerate(model.layer2):
        layer.register_forward_hook(get_features(f'layer2_{idx}'))
    for idx, layer in enumerate(model.layer3):
        layer.register_forward_hook(get_features(f'layer3_{idx}'))
    for idx, layer in enumerate(model.layer4):
        layer.register_forward_hook(get_features(f'layer4_{idx}'))

    # 모델에 이미지 통과
    with torch.no_grad():
        _ = model(image.unsqueeze(0))

    # 특징 맵 시각화
    plt.figure(figsize=(20, 10))
    for idx, (name, feature) in enumerate(features.items(), 1):
        plt.subplot(3, 6, idx)
        # 각 층의 첫 번째 채널만 시각화
        plt.imshow(feature[0, 0].cpu(), cmap='viridis')
        plt.title(f'Layer: {name}')
        plt.axis('off')
    
    plt.tight_layout()
    plt.show()
    
    return features

model, test_image, label, pred, classes = get_trained_model_and_test_image()

# 원본 이미지 시각화
plt.figure(figsize=(4, 4))
plt.imshow(test_image.squeeze(), cmap='gray')
plt.title(f'Class: {classes[label]}')
plt.axis('off')
plt.show()

print(f"이미지 shape: {test_image.shape}")
print(f"실제 클래스: {classes[label]} (레이블: {label})")
print(f"예측 클래스: {classes[pred]} (레이블: {pred})")

# # ResNet 모델에 이미지 통과시키고 특징 맵 시각화
# model = ResNet18(in_channels=1, num_classes=10)
# model.load_state_dict(torch.load('../../models/resnet18_fashion.pth'))
# model.eval()

features = visualize_features(model, test_image)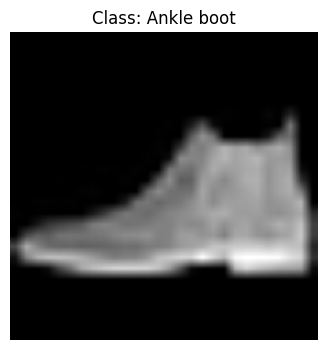

이미지 shape: torch.Size([1, 224, 224])
실제 클래스: Ankle boot (레이블: 9)
예측 클래스: Ankle boot (레이블: 9)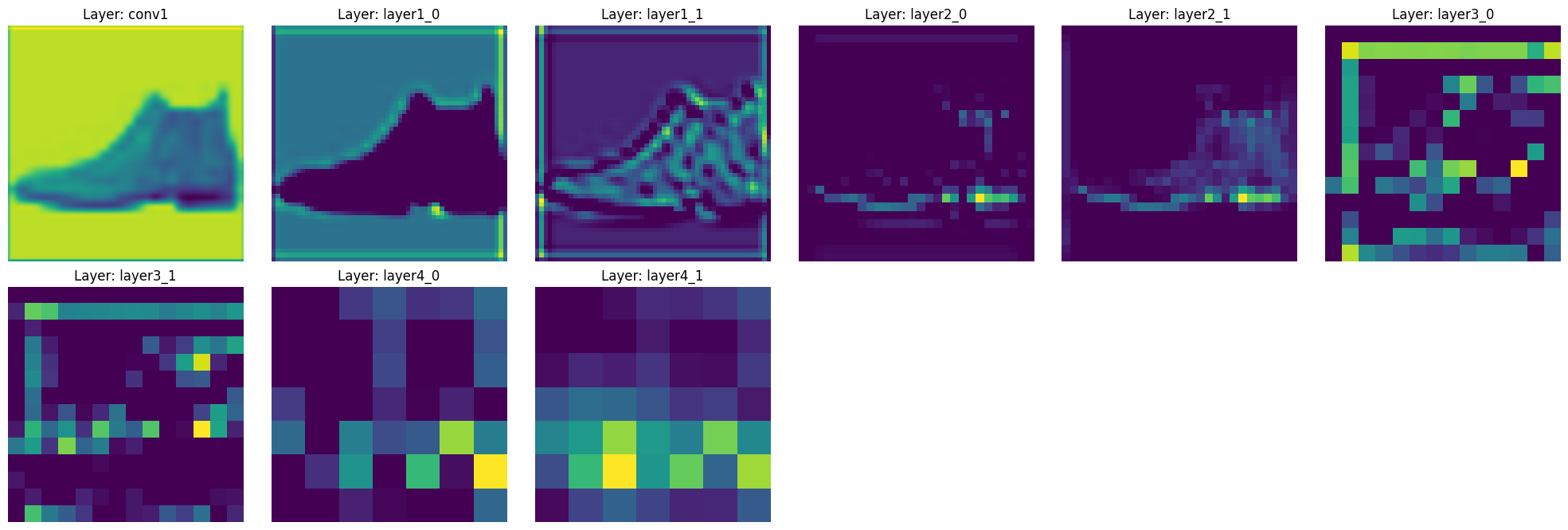

Durch die Ausführung dieses Codes können Sie beobachten, wie die Merkmale sich während des Passierens der Hauptschichten von ResNet-18 verändern.

1. Anfängliche Faltung (conv1): Extraktion grundlegender Forminformationen, Detektion niedrigstufiger Merkmale wie Kanten und Texturen
2. layer1 (anfänglicher Residualblock): Kombination lokaler Merkmale und Beginn der Zusammensetzung einfacher Muster
3. layer2: Die Größe der Merkmalskarten verringert sich, während die Anzahl der Kanäle steigt und komplexere Muster erkannt werden
4. layer3: Der Abstraktionsgrad erhöht sich, wodurch partielle Objektmerkmale detektiert werden können
5. layer4 (letzter Residualblock): Extraktion abstrakter, hochstufiger Merkmale, die für die Klassifikation notwendig sind

Diese hierarchische Merkmalsextraktion ist einer der Kernvorteile von ResNet. Dank der Skip-Verbindungen kann beobachtet werden, dass die Merkmale jeder Schicht gut erhalten bleiben und sich allmählich abstrahieren.

Klicken Sie hier, um den Inhalt anzuzeigen (Deep Dive: Inception-Modul - Vielfalt und Effizienz in CNNs erhöhen)

Inception-Modul - Vielfalt und Effizienz in CNNs hinzufügen

Das Inception-Modul ist ein zentrales Bauteil von GoogLeNet[^1], dem Sieger des ImageNet Large Scale Visual Recognition Challenge (ILSVRC) 2014. Dieses Modul präsentierte einen neuen Ansatz für die herkömmliche CNN-Architektur, ähnlich wie “Network in Network”. Während ResNet das Problem der “Tiefe” löste, adressierte das Inception-Modul gleichzeitig zwei wichtige Herausforderungen: “Vielfalt” und “Effizienz”. In diesem Deep Dive analysieren wir die Kernideen des Inception-Moduls, seine mathematischen Prinzipien sowie seinen Evolutionsprozess. Wir betrachten auch, wie es den Bereich des Deep Learnings, insbesondere die Entwurfsarchitektur von CNNs, beeinflusst hat.

Kernidee des Inception-Moduls: “Multi-Scale” Feature Extraction

Das Inception-Modul bietet eine elegante Lösung für dieses Problem. Es verwendet verschieden große Filter parallel und fügt die Ergebnisse (Feature Maps) zusammen.

Kernidee:

1. Verschiedene Filter: Anwenden verschiedener Convolutional Filters, wie 1x1, 3x3, 5x5, auf dieselbe Eingabe.
2. Parallele Verarbeitung: Jeder Filter führt unabhängig die Convolution Operation durch.
3. Zusammenführung (Concatenation): Fügt die Feature Maps, die von jedem Filter erzeugt wurden, entlang der Kanalachse zusammen.
4. 1x1 Convolution: Reduziert den Berechnungsaufwand, fügt Nichtlinearität hinzu und mischt Informationen zwischen Kanälen. (Funktion als “Bottleneck Layer”)

Inception Modul v1 (GoogLeNet, 2014)

Die erste Version des Inception-Moduls (GoogLeNet, [^1]) hat folgende Struktur:

• Eingabe: Feature Map vom vorherigen Layer
• Parallele Zweige (Branches):
  • 1x1 Convolution
  • 1x1 Convolution -> 3x3 Convolution
  • 1x1 Convolution -> 5x5 Convolution
  • 3x3 Max Pooling -> 1x1 Convolution
• Ausgabe: Zusammenführen (Concatenate) der Ausgaben jeder Zweige entlang der Kanalachse

Rolle der 1x1 Convolution:

Die 1x1 Convolution spielt eine sehr wichtige Rolle im Inception-Modul.

• Dimensionsreduktion (Dimensionality Reduction): Die 1x1 Convolution wird verwendet, um die Anzahl der Kanäle zu reduzieren. Durch die Verwendung einer 1x1 Convolution vor einer 3x3 oder 5x5 Convolution kann der Berechnungsaufwand erheblich reduziert werden. (Bottleneck Layer)
• Hinzufügen von Nichtlinearität: Indem eine Aktivierungsfunktion wie ReLU nach der 1x1 Convolution hinzugefügt wird, kann nichtlineare Dynamik dem Netzwerk hinzugefügt werden.
• Mischen von Informationen zwischen Kanälen: Die 1x1 Convolution berechnet lineare Kombinationen der Eingangskanäle und führt so zu einem Mischen von Informationen zwischen den Kanälen.

Grenzen des Inception Moduls v1:

• 5x5 Convolutions sind immer noch rechenintensiv.
• Pooling Operationen reduzieren die Dimension, können aber auch Informationsverluste verursachen.

Inception Modul v2 & v3 (2015)

Inception v2 und v3 führten folgende Ideen ein, um die Grenzen von v1 zu überwinden [^2]. * Faktorisierung: 5x5-Faltung in zwei 3x3-Faltungen aufteilen. (Berechnungsaufwand verringern) * Asymmetrische Faltung: 3x3-Faltung in eine 1x3- und eine 3x1-Faltung aufteilen. * Nebenklassifikator: Hinzufügen eines Nebenklassifikators (auxiliary classifier) während des Trainings, um das Problem der Gradientenverschwindung zu mildern und das Lernen zu beschleunigen. (in v3 entfernt) * Label Smoothing: Hinzufügen einer geringfügigen Rauschkomponente zu den richtigen Labels, um das Übermaß an Selbstsicherheit des Modells (overconfidence) zu vermeiden.

Inception-Modul v4 (2016)

Inception-v4 führt die Inception-ResNet-Module ein und kombiniert die Inception-Module mit den Residualverbindungen (residual connections) der ResNet [^3].

Xception (2017)

Xception (“Extreme Inception”) ist ein Modell, das die Idee der Inception-Module auf den Extremfall ausdehnt[^4]. Es verwendet Tiefenweise Separable Faltungen (Depthwise Separable Convolutions), um die kanalweise räumliche Faltung (depthwise convolution) von der kanalübergreifenden Faltung (pointwise convolution, 1x1 conv) zu trennen.

Mathematische Darstellung (Inception v1)

Die einzelnen Zweige des Inception-Moduls können wie folgt dargestellt werden:

• Zweig 1: \(\text{Output}_1 = \text{Conv}_{1x1}(\text{Input})\)
• Zweig 2: \(\text{Output}_2 = \text{Conv}_{3x3}(\text{Conv}_{1x1}(\text{Input}))\)
• Zweig 3: \(\text{Output}_3 = \text{Conv}_{5x5}(\text{Conv}_{1x1}(\text{Input}))\)
• Zweig 4: \(\text{Output}_4 = \text{Conv}_{1x1}(\text{MaxPool}(\text{Input}))\)
• Ausgabe: \(\text{Concatenate}(\text{Output}_1, \text{Output}_2, \text{Output}_3, \text{Output}_4)\)

Hierbei steht \(\text{Conv}_{NxN}\) für eine Faltung mit einem \(N \times N\)-Kernel und \(\text{MaxPool}\) für den Max-Pooling-Vorgang.

Ähnlichkeit zur Wavelet-Transformation

Der multi-scale Ansatz des Inception-Moduls weist Parallelen zur Wavelet-Transformation (wavelet transform) auf. Die Wavelet-Transformation ist eine Methode, um ein Signal in verschiedene Frequenzkomponenten zu zerlegen. Die einzelnen Filter (1x1, 3x3, 5x5) des Inception-Moduls können als Extraktion verschiedener Frequenzbänder oder -skalen interpretiert werden. So kann die 1x1-Faltung hohe Frequenzen, die 3x3-Mittelwerte und die 5x5 tiefere Frequenzen erfassen.

Vorteile des Inception-Moduls

• Extraktion von Merkmalen unterschiedlicher Skalen: Durch gleichzeitige Verwendung verschiedener Filtergrößen werden Merkmale unterschiedlicher Größen in Bildern effektiv erfasst.
• Berechnungseffizienz: Die Verwendung von 1x1-Faltungen zur Dimensionsreduktion verringert den Berechnungsaufwand, während die Ausdrucksfähigkeit beibehalten bleibt.
• Leistungsfähig: Es erzielte Top-Performance auf dem ImageNet-Datensatz.

Einfluss auf das Deep-Learning-Ökosystem

Inception-Modul hat eine neue Perspektive auf die Gestaltung von CNN-Architekturen gebracht. Es zeigte nicht nur die Bedeutung des “tieferen Gehens (deeper)”, sondern auch das “breiter Gehende (wider)” und das “vielfältigere Gehende (more diverse)”. Die Idee hinter Inception-Modulen hat auch die Entwicklung leichtgewichtiger Modelle wie MobileNet, ShuffleNet beeinflusst.

Einfache Implementierung eines Inception-Moduls (PyTorch)

import torch
import torch.nn as nn
import torch.nn.functional as F

class InceptionModule(nn.Module):
    def __init__(self, in_channels, out_channels_1x1, out_channels_3x3_reduce,
                 out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5,
                 out_channels_pool):
        super().__init__()

        # 1x1 Conv-Branch
        self.branch1x1 = nn.Conv2d(in_channels, out_channels_1x1, kernel_size=1)

        # 1x1 Conv -> 3x3 Conv-Branch
        self.branch3x3_reduce = nn.Conv2d(in_channels, out_channels_3x3_reduce, kernel_size=1)
        self.branch3x3 = nn.Conv2d(out_channels_3x3_reduce, out_channels_3x3, kernel_size=3, padding=1)

        # 1x1 Conv -> 5x5 Conv-Branch
        self.branch5x5_reduce = nn.Conv2d(in_channels, out_channels_5x5_reduce, kernel_size=1)
        self.branch5x5 = nn.Conv2d(out_channels_5x5_reduce, out_channels_5x5, kernel_size=5, padding=2)

        # 3x3 Max-Pool -> 1x1 Conv-Branch
        self.branch_pool = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.branch_pool_proj = nn.Conv2d(in_channels, out_channels_pool, kernel_size=1)

    def forward(self, x):
        branch1x1 = F.relu(self.branch1x1(x))

        branch3x3 = F.relu(self.branch3x3_reduce(x))
        branch3x3 = F.relu(self.branch3x3(branch3x3))

        branch5x5 = F.relu(self.branch5x5_reduce(x))
        branch5x5 = F.relu(self.branch5x5(branch5x5))

        branch_pool = F.relu(self.branch_pool_proj(self.branch_pool(x)))

        outputs = [branch1x1, branch3x3, branch5x5, branch_pool]
        return torch.cat(outputs, 1)  # Concatenate along the channel dimension

Beispielverwendung

in_channels = 3 # Beispiel Eingangskanäle out_channels_1x1 = 64 out_channels_3x3_reduce = 96 out_channels_3x3 = 128 out_channels_5x5_reduce = 16 out_channels_5x5 = 32 out_channels_pool = 32

inception_module = InceptionModule(in_channels, out_channels_1x1, out_channels_3x3_reduce, out_channels_3x3, out_channels_5x5_reduce, out_channels_5x5, out_channels_pool)

Beispiel Eingangstensor (Batch-Größe, Kanäle, Höhe, Breite)

input_tensor = torch.randn(1, in_channels, 28, 28) output_tensor = inception_module(input_tensor) print(output_tensor.shape) # Überprüfen der Ausgabeform

Dieser Code implementiert die grundlegende Struktur eines Inception-Moduls (v1) in PyTorch. `torchvision.models` oder das `timm`-Paket bieten fortgeschrittene Versionen des Inception-Netzwerks (Inception-v3, Inception-v4, Inception-ResNet usw.), die in echten Projekten bevorzugt verwendet werden sollten.

---

[1]: Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., ... & Rabinovich, A. (2015). Going deeper with convolutions. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1-9).

[2]: Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., & Wojna, Z. (2016). Rethinking the inception architecture for computer vision. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 2818-2826).

[3]: Szegedy, C., Ioffe, S., Vanhoucke, V., & Alemi, A. A. (2017). Inception-v4, inception-resnet and the impact of residual connections on learning. In *Thirty-first AAAI conference on artificial intelligence*.

[4]: Chollet, F. (2017). Xception: Deep learning with depthwise separable convolutions. In *Proceedings of the IEEE conference on computer vision and pattern recognition* (pp. 1251-1258).
:::

## 7.3 EfficientNet: Effizientes Modellskalieren

> **Herausforderung:** Wie kann die Leistung eines Modells maximiert werden, während gleichzeitig der Berechnungsbedarf (Anzahl der Parameter, FLOPS) minimiert wird?
>
> **Sorgen der Forscher:** Mit der Einführung von ResNet wurde es möglich, tiefe Netzwerke zu trainieren. Allerdings gab es bislang keine systematische Methode, um die Größe des Modells anzupassen. Das einfache Hinzufügen von Schichten oder das Erhöhen der Anzahl der Kanäle kann den Berechnungsbedarf erheblich steigern. Die Forscher suchten danach, die optimale Balance zwischen Tiefe (depth), Breite (width) und Auflösung (resolution) des Modells zu finden, um so unter gegebenen Rechenressourcen die beste Leistung zu erzielen.

### 7.3.1 Compound Scaling: Balance von Tiefe, Breite und Auflösung

Das Kernkonzept von EfficientNet ist "Compound Scaling". Während frühere Studien dazu neigten, entweder nur die Tiefe, Breite oder Auflösung des Modells zu adjustieren, stellte EfficientNet fest, dass es effektiver ist, diese drei Faktoren *gleichzeitig und balanciert* anzupassen.

*   **Tiefe (Depth):** Die Anzahl der Schichten im Netzwerk. Tiefere Netzwerke können komplexere Merkmale lernen, sind aber anfällig für Gradientenverschwinden/Explosion und Overfitting.
*   **Breite (Width):** Die Anzahl der Kanäle (Filter) pro Schicht. Breitere Netzwerke können feinere Merkmale (fine-grained features) lernen, was zu einem höheren Berechnungsbedarf, mehr Parametern und erhöhtem Risiko von Overfitting führt.
*   **Auflösung (Resolution):** Die Größe der Eingabebilder. Bilder mit höherer Auflösung enthalten mehr Informationen, können aber den Berechnungsbedarf erheblich steigern.

EfficientNet zeigte experimentell, dass die drei Faktoren miteinander verbunden sind und es effektiver ist, sie *balanciert* zusammen anzupassen, anstatt nur einen einzigen Faktor zu verändern. Zum Beispiel, wenn die Bildauflösung verdoppelt wird, sollten Tiefe und Breite angemessen erhöht werden, damit das Netzwerk feinere Muster lernen kann. Das einfache Verdoppeln der Auflösung kann zu minimalen oder sogar schlechteren Leistungsverbesserungen führen.

In der EfficientNet-Paper wurde das Problem des Modellskalierens als Optimierungsproblem definiert, und die Beziehungen zwischen Tiefe (depth), Breite (width) und Auflösung (resolution) wurden durch folgende Formel ausgedrückt.

Zunächst wird ein CNN-Modell $\mathcal{N}$ bezeichnet. Die $i$-te Schicht kann als Funktions transformation $Y_i = \mathcal{F}_i(X_i)$ dargestellt werden, wobei die Form von $X_i$ als $<H_i, W_i, C_i>$ angegeben wird, was jeweils für Höhe (height), Breite (width) und Anzahl der Kanäle (channel) steht.

Das gesamte CNN-Modell $\mathcal{N}$ kann als Komposition von Schichten dargestellt werden

$\mathcal{N} = \mathcal{F}_k \circ \mathcal{F}_{k-1} \circ ... \circ \mathcal{F}_1 = \bigodot_{i=1...k} \mathcal{F}_i$

Bei der üblichen CNN-Designs wird der Fokus darauf gelegt, die optimale Schichtoperation $\mathcal{F}_i$ zu finden. EfficientNet konzentriert sich jedoch darauf, bei festgelegten Schichtoperationen die Länge ($\hat{L}_i$), Breite ($\hat{C}_i$) und Auflösung ($\hat{H}_i, \hat{W}_i$) des Netzwerks anzupassen. Dazu wird ein Baseline-Netzwerk $\hat{\mathcal{N}}$ definiert und mit Skalierungsfaktoren multipliziert, um das Modell zu erweitern.
Referenznetzwerk: $\hat{\mathcal{N}} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{L_i}(X_{<H_i, W_i, C_i>})$

EfficientNet strebt an, das folgende Optimierungsproblem zu lösen:

$\underset{\mathcal{N}}{maximize}\quad Accuracy(\mathcal{N})$

$subject\ to\quad \mathcal{N} = \bigodot_{i=1...s} \hat{\mathcal{F}}_i^{d \cdot \hat{L}_i}(X_{<r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i>})$

$Memory(\mathcal{N}) \leq target\_memory$

$FLOPS(\mathcal{N}) \leq target\_flops$

Hierbei sind $d$, $w$, $r$ die Skalierungsfaktoren für Tiefe, Breite und Auflösung.

EfficientNet schlägt eine **Compound Scaling** Methode vor, um dieses Problem zu lösen. Diese Methode vereinfacht das komplexe Optimierungsproblem, indem sie die Genauigkeit maximiert, während gleichzeitig alle Ressourcenbeschränkungen (resource constraints) erfüllt werden.

$\begin{aligned}
& \text{Tiefe: } d = \alpha^{\phi} \\
& \text{Breite: } w = \beta^{\phi} \\
& \text{Auflösung: } r = \gamma^{\phi} \\
& \text{subject to } \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\
& \alpha \geq 1, \beta \geq 1, \gamma \geq 1
\end{aligned}$

*   $\phi$ (phi) ist ein von Benutzern spezifizierter Skalierungsfaktor (compound coefficient), der die gesamte Modellgröße steuert.
*   $\alpha$, $\beta$, $\gamma$ sind Konstanten, die bestimmen, um wie viel die Tiefe, Breite und Auflösung erhöht werden. Diese Werte werden durch eine kleine Raster-Suche (small grid search) festgelegt. ($\alpha$, $\beta$, $\gamma$ Werte werden gefunden, indem $\phi=1$ festgelegt und eine kleine Suche durchgeführt wird.)
*   Die Nebenbedingung ($α ⋅ β² ⋅ γ² ≈ 2$) stellt sicher, dass die FLOPS des Modells bei jeder Erhöhung von $ϕ$ um eins etwa verdoppelt werden. Diese Nebenbedingung wurde festgelegt, da die FLOPS linear mit der Tiefe und quadratisch mit der Breite und Auflösung steigen.

Mit dieser Compound Scaling Methode können Benutzer die Modellgröße leicht durch Anpassen des $ϕ$-Werts steuern und ein effektives Gleichgewicht zwischen Modellleistung und Effizienz erzielen.

### 7.3.2 EfficientNet Architektur

EfficientNet nutzt AutoML (Neural Architecture Search, NAS) Technologien, um das optimale Basismodell (baseline model), EfficientNet-B0 zu finden, und wendet hierauf Compound Scaling an, um Modelle verschiedener Größen (B1 bis B7 und größere L2) zu erzeugen.

**EfficientNet-B0 Architektur:**

EfficientNet-B0 basiert auf MBConv-Blöcken (Mobile Inverted Bottleneck Convolution), die von MobileNetV2 inspiriert sind. Die MBConv-Blöcke haben folgende Struktur, um die Berechnungseffizienz zu erhöhen.
1.  **Expansion (1x1 Conv):** Erweitert die Anzahl der Eingangskanäle (Expansionsfaktor, üblicherweise 6). Durch das Erhöhen der Kanalanzahl mit einer 1x1-Konvolution kann man die Rechenkosten für nachfolgende Operationen (depthwise convolution) relativ reduzieren und gleichzeitig die Ausdrucksstärke erhöhen.

2.  **Depthwise Separable Convolution:**
    *   **Depthwise Convolution (3x3):** Führt eine *unabhängige* räumliche Konvolution für jeden Eingangskanal durch. Im Gegensatz zu einer normalen Konvolution findet kein Informationsmix zwischen den Kanälen statt.
    *   **Pointwise Convolution (1x1 Conv):** Mischung der Informationen zwischen den Kanälen durch eine 1x1-Konvolution.

    Depthwise separable convolution kann die Anzahl der Parameter und Berechnungen im Vergleich zu einer normalen Konvolution erheblich reduzieren.

3.  **Squeeze-and-Excitation (SE) Block:** Lernprozess zur Bestimmung der Wichtigkeit zwischen den Kanälen, um wichtige Kanäle hervorzuheben. Der SE-Block verwendet globales Mittelwertpooling (global average pooling), um die Informationen jedes Kanals zusammenzufassen, und zwei vollständig verbundene Schichten, um für jeden Kanal ein Gewicht zu berechnen.

4.  **Projection (1x1 Conv):** Reduziert die Anzahl der Kanäle wieder auf den ursprünglichen Wert. (für residual connection)

5.  **Residual Connection:** Addiert Eingang und Ausgang. (wenn die Anzahl der Eingangs- und Ausgabekanäle gleich ist, bei stride=1). Kernidee von ResNet.

Im Folgenden finden Sie ein Beispiel für die Implementierung eines MBConv-BLOCKS von EfficientNet-B0 in PyTorch. (Die vollständige Implementierung von EfficientNet-B0 wird hier weggelassen. Sie können es aus der torchvision- oder timm-Bibliothek laden.)

::: {#cell-46 .cell}
``` {.python .cell-code}
import torch
import torch.nn as nn
import torch.nn.functional as F

class MBConvBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride, expand_ratio=6, se_ratio=0.25, kernel_size=3):
        super().__init__()

        self.stride = stride
        self.use_residual = (in_channels == out_channels) and (stride == 1) # 잔차 연결 조건

        expanded_channels = in_channels * expand_ratio

        # Expansion (1x1 conv)
        self.expand_conv = nn.Conv2d(in_channels, expanded_channels, kernel_size=1, bias=False)
        self.bn0 = nn.BatchNorm2d(expanded_channels)

        # Depthwise convolution
        self.depthwise_conv = nn.Conv2d(expanded_channels, expanded_channels, kernel_size=kernel_size,
                                       stride=stride, padding=kernel_size//2, groups=expanded_channels, bias=False)
                                       # groups=expanded_channels: depthwise conv
        self.bn1 = nn.BatchNorm2d(expanded_channels)

        # Squeeze-and-Excitation
        num_reduced_channels = max(1, int(in_channels * se_ratio))  # 최소 1개는 유지
        self.se_reduce = nn.Conv2d(expanded_channels, num_reduced_channels, kernel_size=1)
        self.se_expand = nn.Conv2d(num_reduced_channels, expanded_channels, kernel_size=1)

        # Pointwise convolution (projection)
        self.project_conv = nn.Conv2d(expanded_channels, out_channels, kernel_size=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)

    def forward(self, x):
        identity = x

        # Expansion
        out = F.relu6(self.bn0(self.expand_conv(x)))

        # Depthwise separable convolution
        out = F.relu6(self.bn1(self.depthwise_conv(out)))

        # Squeeze-and-Excitation
        se = out.mean((2, 3), keepdim=True)  # Global Average Pooling
        se = F.relu6(self.se_reduce(se))
        se = torch.sigmoid(self.se_expand(se))
        out = out * se  # 채널별 가중치 곱

        # Projection
        out = self.bn2(self.project_conv(out))

        # Residual connection
        if self.use_residual:
            out = out + identity

        return out

# Example usage
# in_channels = 32
# out_channels = 16
# stride = 1
# mbconv_block = MBConvBlock(in_channels, out_channels, stride)
# input_tensor = torch.randn(1, in_channels, 224, 224)  # Example input
# output_tensor = mbconv_block(input_tensor)
# print(output_tensor.shape)

7.3.3 Leistung und Einfluss von EfficientNet

EfficientNet hat bei der ImageNet-Klassifikation eine höhere Genauigkeit erreicht als traditionelle CNN-Modelle (ResNet, DenseNet, Inception usw.), dabei weitaus weniger Parameter und Berechnungen benötigend. Die folgende Tabelle vergleicht die Leistung von EfficientNet mit anderen Modellen.

Model	Top-1 Accuracy	Top-5 Accuracy	Parameters	FLOPS
ResNet-50	76.0%	93.0%	25.6M	4.1B
DenseNet-169	76.2%	93.2%	14.3M	3.4B
Inception-v3	77.9%	93.8%	23.9M	5.7B
EfficientNet-B0	77.1%	93.3%	5.3M	0.39B
EfficientNet-B1	79.1%	94.4%	7.8M	0.70B
EfficientNet-B4	82.9%	96.4%	19.3M	4.2B
EfficientNet-B7	84.3%	97.0%	66M	37B
EfficientNet-L2*	85.5%	97.7%	480M	470B

* Verwendung von Noisy Student Training

Wie in der Tabelle ersichtlich, erreichte EfficientNet-B0 eine höhere Genauigkeit als ResNet-50 mit weniger Parametern und FLOPS. EfficientNet-B7 erreichte bei ImageNet eine Top-1-Genauigkeit von 84.3% (damals state-of-the-art), war aber weiterhin effizienter als andere große Modelle.

Hauptbeiträge von EfficientNet:

• Verbundskalierung (Compound Scaling): Eine neue Methodik zur ausgewogenen Anpassung der Tiefe, Breite und Auflösung des Modells wurde vorgestellt, um das Verständnis der Beziehung zwischen Modellgröße und Leistung zu vertiefen.
• Effizientes Modell-Design: EfficientNet-B0, das mit AutoML (NAS) gefunden wurde, zeigte eine höhere Effizienz und Leistungsfähigkeit im Vergleich zu manuell entwickelten Modellen.
• Praktikabilität: EfficientNet bietet Modelle unterschiedlicher Größen (B0 bis B7, L2), sodass Benutzer ein Modell auswählen können, das ihren Rechenressourcen und Leistungsanforderungen entspricht.

Einfluss auf Wissenschaft und Industrie:

EfficientNet hat die Forschung zur Modellverkleinerung und Effizienz gefördert und wird in Ressourcenbeschränkten Umgebungen wie Mobilgeräte und eingebettete Systeme häufig verwendet, um Deep-Learning-Modelle bereitzustellen. Die Idee der verbundskalierung von EfficientNet wurde auf andere Modelle angewendet, um Leistungsverbesserungen zu erzielen. Nach EfficientNet wurden intensive Forschungen wie EfficientNetV2, MobileNetV3 und RegNet durchgeführt, die sich auf Effizienz konzentrieren.

Grenzen:

• Es fehlt eine vollständige theoretische Erklärung dafür, warum die mit AutoML (NAS) gefundenen EfficientNet-B0-Architekturen effektiver sind als andere Architekturen.
• Die Methode der verbundskalierung kann nicht für alle Arten von CNN-Architekturen und Aufgaben als optimal garantiert werden. Trotzdem wird EfficientNet als wichtiger Meilenstein in der Geschichte des Deep Learnings angesehen, da es eine neue Perspektive auf die Gestaltung von CNN-Modellen gebracht und die Effizienz der Modelle revolutionär verbessert hat.

Fazit

In diesem Kapitel haben wir den Hintergrund der Entstehung und Entwicklung von Faltungsneuronalen Netzen (CNN) sowie die wichtigsten Fortschritte in Form von ResNet, Inception-Moduln und EfficientNet untersucht.

CNNs zeigten bei der Bilderkennung mit LeNet-5 und AlexNet große Erfolge, stießen jedoch auf Schwierigkeiten beim Lernen tiefer Netzwerke. ResNet löste dieses Problem durch residuelle Verbindungen und ermöglichte eine revolutionäre Vertiefung. Inception-Module erhöhten die Vielfalt und Effizienz der Merkmalsextraktion durch parallele Nutzung von Filtern unterschiedlicher Größen, während EfficientNet ein systematisches Vorgehen zur ausgewogenen Anpassung von Tiefe, Breite und Auflösung des Modells vorschlug.

Diese Innovationen trugen maßgeblich dazu bei, dass CNNs nicht nur in der Bilderkennung, sondern auch in verschiedenen Computer-Vision-Aufgaben eine zentrale Rolle spielen. Allerdings waren CNNs gut darin, räumliche lokale Muster zu erfassen, aber weniger geeignet für sequenzielle Daten, insbesondere solche, bei denen die Reihenfolge und langfristige Abhängigkeiten (long-range dependencies) wichtig sind, wie beispielsweise in der natürlichen Sprachverarbeitung.

Im nächsten Kapitel werden wir die Transformer-Architektur untersuchen, die ohne Verwendung von Faltungsvorgängen und Pooling-Operationen und nur mit dem Attention-Mechanismus die Beziehungen zwischen Elementen in einer Sequenz modelliert. Transformer hat eine erhebliche Leistungssteigerung im Bereich der natürlichen Sprachverarbeitung gebracht und seine Wirkungskraft inzwischen auch auf andere Bereiche wie Computer-Vision und Sprachverarbeitung ausgedehnt. Ebenso wie die residuellen Verbindungen von ResNet die Tiefebegrenzung von CNNs überwunden haben, hat der Attention-Mechanismus von Transformer neue Möglichkeiten für die Verarbeitung sequenzieller Daten eröffnet.

Übungsaufgaben

Grundlegende Aufgaben

1. Erkläre die Rolle der Faltung (Convolution) in der Bildverarbeitung und beschreibe diese spezifisch anhand eines Beispiels wie dem Sobel-Filter.
2. Erläutere die Funktion und Vorteile von Pooling-Layern in CNNs und vergleiche den Unterschied zwischen Max-Pooling und Average-Pooling.
3. Erkläre, wie Residual Connections im ResNet tiefen Netzwerken beim Lernen helfen, insbesondere im Kontext der Probleme Gradient Vanishing/Exploding.
4. Beschreibe die Kernidee des Inception-Moduls, nämlich “die Verwendung von Filtern unterschiedlicher Größen” und die Rolle von “1x1-Faltungen”.
5. Erkläre, was “compound scaling” im EfficientNet ist, und vergleiche es mit traditionellen Methoden zur Anpassung der Modellgröße (Tiefe, Breite, Auflösung) in Bezug auf Vorteile.

Angewandte Aufgaben

1. Implementiere ein einfaches CNN-Modell in PyTorch und trainiere sowie evaluiere es mit dem MNIST-Datensatz. (Datenladevorgang, Modelldefinition, Trainingsloop, Evaluationsloop einschließen)
2. Lade das ResNet-18-Modell aus torchvision.models und führe Transfer Learning auf dem CIFAR-10-Datensatz durch, dann bewerte die Leistung. (Datenpräprocessing, Modellladevorgang, Fine-Tuning, Evaluierung)
3. Nutze die in expertai_src bereitgestellte Funktion show_filter_effects, um visuell den Einfluss verschiedener Filter (z.B. Blur, Sharpening, Kanten erkennung) auf Bilder zu vergleichen und die Eigenschaften jedes Filters zu beschreiben.
4. Entferne die Residual Connections im gegebenen ResNet-Code (BasicBlock, Bottleneck) und messe die Leistungsänderungen beim Training mit den gleichen Daten, dann analysiere die Gründe dafür.
5. Implementiere eine 2D-Faltungsberechnung nach dem Vorbild der SimpleConv2d-Klasse. (Verwendung von NumPy oder PyTorch’s tensor-Operationen, Verbot der Verwendung von torch.nn.Conv2d).

Fortgeschrittene Aufgaben

1. Erkläre mathematisch die Ursachen für das Problem des Gradient Vanishing/Exploding in tiefen CNNs und beschreibe, wie Residual Connections im ResNet, Batch Normalization und 1x1-Faltungen im Inception-Modul dieses Problem jeweils mildern.
2. Lies die ResNet-, Inception- und EfficientNet-Papiere und vergleiche und analysiere die Kernideen der einzelnen Modelle. (Stärken und Schwächen jedes Modells, Beziehungen zueinander, Einfluss auf nachfolgende Forschung)
3. Leite die Formel für das compound scaling im EfficientNet her (oder erkläre sie detailliert unter Verweis auf den Paper) und beschreibe, wie man unter gegebenen Rechenressourcenbeschränkungen die optimale Modellgröße bestimmt.
4. Erkläre die Beziehung zwischen Gaußprozessen und Deep Kernel Learning (DKL) und beschreibe, welche Vorteile DKL im Vergleich zu traditionellen CNNs und GPs hat.
5. Finde mindestens ein Beispiel in CNN-bezogenen Publikationen aus den letzten 1-2 Jahren, das die Ideen von ResNet, Inception oder EfficientNet weiterentwickelt, fasst dessen Inhalte zusammen und gib deine eigene Meinung dazu ab. (Beispiel: ConvNeXt, NFNet)

Klicken Sie hier, um den Inhalt anzuzeigen (Lösungen zu Übungsaufgaben)

Übungslösungen

Grundlegende Aufgaben

1. Konvolution und Sobel-Filter:
   • Rolle: Die Konvolution extrahiert Merkmale durch die Berechnung von gewichteten Summen der Pixelwerte und Filterwerte an jeder Position, wobei der Filter über das Bild gleitet.
   • Sobel-Filter: Wird zur Kantenerkennung in Bildern verwendet. Vertikale/Horizontal-Sobel-Filter erkennen jeweils Helligkeitsänderungen in vertikaler/horizontaler Richtung.
2. Pooling-Layer:
   • Rolle/Vorteile: Verringert die Größe (räumliche Dimension) der Merkmalskarten, um den Berechnungsaufwand zu reduzieren und Translationsinvarianz zu erhöhen, was Overfitting verhindert.
   • Max-Pooling: Wählt das Maximum in einem Bereich aus. Behält die auffälligsten Merkmale bei.
   • Average-Pooling: Berechnet den Mittelwert in einem Bereich. Ist weniger anfällig für Rauschen.
3. ResNet Residual-Verbindungen:
   • Residual-Verbindung: Eine “Shortcut”-Verbindung, die den Eingangswert direkt zum Output addiert. \(H(x) = F(x) + x\)
   • Milderung von Gradientenverschwinden/-explosion: Da der Gradient über die Residual-Verbindung direkt weitergeleitet wird, verbreiten sich die Gradienten auch in tiefen Netzen gut. Es erleichtert dem neuronalen Netzwerk das Lernen einer Identitätsabbildung (identity mapping, \(F(x) = 0\)).
4. Inception-Modul:
   • Verschiedene Filtergrößen: Verwendet parallele Filter verschiedener Größen wie 1x1, 3x3, 5x5, um gleichzeitig Merkmale verschiedener Größen in Bildern zu erfassen.
   • 1x1-Konvolution: Reduziert die Dimensionen zwischen Kanälen und fügt Nichtlinearität hinzu. Es reduziert den Berechnungsaufwand, während es die Ausdrucksstärke des Modells erhöht (funktioniert als “Bottleneck-Schicht”).
5. EfficientNet Compound Scaling:
   • Compound Scaling: Methode, um Tiefe (depth), Breite (width) und Auflösung (resolution) des Netzes ausgewogen gleichzeitig zu erhöhen. Es wird ein einzelner Koeffizient (compound coefficient) verwendet, um die drei Faktoren simultan anzupassen.
   • Vorteile: Bietet eine effizientere Steigerung der Modellleistung im Vergleich zu herkömmlichen Methoden (Änderung eines einzigen Faktors). Ermöglicht es, die Modellgröße so anzupassen, dass optimale Leistung bei gegebenen Rechenressourcen erreicht wird.

Anwendungsbeispiele

1. CNN-Implementierung und MNIST-Training: (Code ausgelassen) Verwendung von PyTorch, um ein CNN-Modell mit nn.Conv2d, nn.ReLU, nn.MaxPool2d und nn.Linear zu bilden und das MNIST-Dataset mithilfe von DataLoader für Training und Evaluation zu laden.

2. Transfer Learning mit ResNet-18: (Code ausgelassen) Aus torchvision.models wird resnet18 geladen, wobei die letzte Schicht (fully connected layer) für CIFAR-100 angepasst wird, und einige Schichten feintuning durchgeführt werden.

3. Analyse von show_filter_effects: (Code ausgelassen) Die Funktion show_filter_effects wendet verschiedene Filter (Gaußscher Weichzeichner, Schärfung, Kantenerkennung, Relieffilter, Sobel X) auf ein gegebenes Bild an und visualisiert die Ergebnisse. Jeder Filter betont oder verändert bestimmte Merkmale des Bildes (Weichzeichnung, Schärfe, Kanten etc.).

4. Entfernen von ResNet-Residual-Verbindungen: (Code ausgelassen) Die Entfernung der Residual-Verbindungen führt zu Schwierigkeiten bei der Trainierung tiefer Netze aufgrund von Gradientenverschwinden/-explosion, was eine Leistungseinbuße zur Folge hat.

5. 2D Konvolution direkt implementieren: (Codeauslassung) Verwenden Sie verschachtelte for-Schleifen, um die elementweise Multiplikation und Summierung des Kernels mit jedem Ort des Eingabetensors durchzuführen. Die Verwendung von Techniken wie im2col zur Transformation in Matrixmultiplikationen kann effizienter sein.

Vertiefende Aufgaben

1. Gradientenverschwinden/-explosion:

   • Ursache: Bei der Rückwärtspropagation werden die Gradienten gemäß der Kettenregel wiederholt multipliziert, was dazu führt, dass die Gradienten in tieferen Schichten sehr klein (Verschwinden) oder groß (Explosion) werden. Wenn der Differentialwert der Aktivierungsfunktion kleiner als 1 ist (z.B. sigmoid, tanh), neigen sie eher zum Verschwinden; wenn er größer als 1 ist, neigen sie eher zur Explosion.
   • ResNet residuelle Verbindungen: Da die Gradienten direkt durch die residuellen Verbindungen übertragen werden, wird das Problem des Gradientenverschwindens/-explodierens gemildert.
   • Batch Normalisierung: Durch die Normalisierung der Eingaben jeder Schicht werden die Eingaben der Aktivierungsfunktion in einen angemessenen Bereich gehalten, was zu einer Reduzierung von Gradientenverschwinden/-explosionen führt.
   • Inception 1x1 Konvolution: Die Anzahl der Kanäle wird reduziert, was die Berechnungsmenge verringert und das Problem des Gradientenverschwindens/-explodierens indirekt mildert. (aufgrund der Verringerung der Parameteranzahl)

2. Vergleich von ResNet, Inception, EfficientNet: (detaillierter Vergleich ausgelassen)

   • ResNet: Erleichtert das Lernen tief verwachsener Netzwerke durch residuelle Verbindungen.
   • Inception: Verwendet parallele Filter verschiedener Größen, um Merkmale auf verschiedenen Skalen zu extrahieren. 1x1-Konvolutionen werden verwendet, um die Berechnungseffizienz zu steigern.
   • EfficientNet: Verbessert Effizienz und Leistung durch Compound Scaling, das Tiefe, Breite und Auflösung des Modells ausgewogen anpasst.

3. EfficientNet Compound Scaling: (Formale Herleitung/detaillierte Erklärung ausgelassen) Verwendung eines compound coefficients (Φ), um die Tiefe (α^Φ), Breite (β^Φ) und Auflösung (γ^Φ) anzupassen. α, β, γ sind Konstanten, die durch kleine Grid-Suchvorgänge gefunden wurden. Nebenbedingung: α ⋅ β² ⋅ γ² ≈ 2.

4. Gaußsche Prozesse (GP) und DKL:

   • GP: Wahrscheinlichkeitsverteilung über Funktionen. Verwendet Kernelfunktionen, um die Kovarianz zwischen Funktionswerten zu definieren. Bietet Unsicherheitsschätzungen durch bayesianische Inferenz.
   • DKL (Deep Kernel Learning): Verwendet Deep Learning (Neuronale Netze), um Merkmale aus Daten zu extrahieren und diese Merkmale als Eingabe für die Kernelfunktion des GP zu verwenden. Kombiniert die Fähigkeit von Deep Learning, Merkmale zu lernen, mit der Fähigkeit von GPs, Unsicherheit zu schätzen.
   • Vorteile: Dateneffizienz, Unsicherheitsschätzungen, flexible Merkmalsrepräsentation.
   • Nachteile: Die Berechnungskomplexität von GPs besteht weiterhin.

5. Neueste CNN-Papiere: (Beispiele: ConvNeXt, NFNet usw. Zusammenfassungen und Meinungen ausgelassen)

Referenzmaterialien

1. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex (Hubel & Wiesel, 1962): Studie über die visuelle Rinde der Katze. Dieses Papier hat das Konzept des Receptive Field in CNNs inspiriert. (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1359523/)
2. The Scientist and Engineer’s Guide to Digital Signal Processing (Steven W. Smith): Buch, das die grundlegenden Prinzipien der digitalen Signalverarbeitung erläutert. Es hilft beim Verstehen von Konzepten wie Faltung und Filter. (http://www.dspguide.com/pdfbook.htm)
3. Gradient-based learning applied to document recognition (LeCun et al., 1998): Verwendung von CNNs für die Texterkennung. Einführung des LeNet-5. (http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf)
4. Deep Residual Learning for Image Recognition (He et al., 2015): Ursprüngliches Paper zu ResNet. (https://arxiv.org/pdf/1512.03385.pdf)
5. Network in Network (Lin et al., 2013): Paper, das die Idee der 1x1-Faltung vorgestellt hat. (https://arxiv.org/pdf/1312.4400.pdf)
6. Very Deep Convolutional Networks for Large-Scale Image Recognition (Simonyan & Zisserman, 2014): VGGNet-Paper. (https://arxiv.org/pdf/1409.1557.pdf)
7. Dive into Deep Learning (Zhang et al., 2023): Kapitel 9 “Convolutional Neural Networks” erklärt die grundlegenden Konzepte von CNNs und ResNet. (https://d2l.ai/chapter_convolutional-neural-networks/index.html)
8. CS231n: Convolutional Neural Networks for Visual Recognition (Stanford University): Vorlesungsmaterialien zu CNNs. (http://cs231n.github.io/convolutional-networks/)
9. Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift (Li et al., 2018): Paper, das die Vorsicht beim gemeinsamen Einsatz von Batch-Normalisierung und Dropout erläutert.
10. Rethinking the Inception Architecture for Computer Vision (Szegedy et al., 2015): Erklärung des Inception-v3-Moduls (https://arxiv.org/abs/1512.00567)
11. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex (Hubel & Wiesel, 1962): Studie über die visuelle Rinde der Katze. Dieses Papier hat das Konzept des Receptiven Felds bei CNNs inspiriert. (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1359523/) 2. The Scientist and Engineer’s Guide to Digital Signal Processing (Steven W. Smith): Ein Buch, das die grundlegenden Prinzipien der digitalen Signalverarbeitung erklärt. Es hilft beim Verständnis von Konzepten wie Faltung und Filtern. (http://www.dspguide.com/pdfbook.htm) 3. Gradient-based learning applied to document recognition (LeCun et al., 1998): Verwendung von CNNs für die Zeichenerkennung. Einführung des LeNet-5. (http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf) 4. Deep Residual Learning for Image Recognition (He et al., 2015): Ursprüngliches Papier über ResNet. (https://arxiv.org/pdf/1512.03385.pdf) 5. Network in Network (Lin et al., 2013): Paper, das die Idee der 1x1-Faltung präsentiert. (https://arxiv.org/pdf/1312.4400.pdf) 6. Very Deep Convolutional Networks for Large-Scale Image Recognition (Simonyan & Zisserman, 2014): VGGNet-Papier. (https://arxiv.org/pdf/1409.1557.pdf) 7. Dive into Deep Learning (Zhang et al., 2023): Kapitel 9 “Convolutional Neural Networks” erklärt grundlegende Konzepte von CNNs und ResNet. (https://d2l.ai/chapter_convolutional-neural-networks/index.html) 8. CS231n: Convolutional Neural Networks for Visual Recognition (Stanford University): Vorlesungsmaterialien zu CNNs. (http://cs231n.github.io/convolutional-networks/) 9. Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift (Li et al., 2018): Papier, das auf die Probleme bei der gemeinsamen Verwendung von Batch-Normalisierung und Dropout eingeht. 10. Rethinking the Inception Architecture for Computer Vision (Szegedy et al., 2015): Beschreibung von Inception-v3 und Inceptions-Modulen. | Deutsch |
    | — | | Dieses Dokument ist eine umfassende Übersicht über die aktuellen Entwicklungen im Bereich des Deep Learnings. Wir untersuchen erfolgreiche Anwendungen von Deep Learning in verschiedenen Bereichen wie Bilderkennung, Spracherkennung und natürlichsprachliche Verarbeitung, um die dahinter liegenden Prinzipien zu verstehen. Darüber hinaus stellen wir verschiedene Methodologien zur Schulung und Optimierung tiefer neuronaler Netze vor. |